题目内容
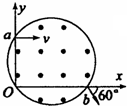
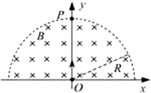
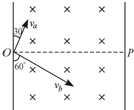
如图所示,再第二象限和第四象限的正方形区域内分别存在着面积相同的匀强磁场,磁感应强度均为B,方向相反,且都垂直与xoy平面;在第一象限内存在着平行与xoy平,沿x轴方向的匀强磁场(图中没有画出);一电子由P(-d,d)点,沿x轴正方向射入磁场区域Ⅰ.(电子质量为m,电荷量为e,sin53°=0.8)
(1)若电子离开磁场区域Ⅰ后直接进入第三象限,求入射速度的范围;
(2)若电子从(0,
)位置射出磁场Ⅰ,接着通过第一象限后直接垂直与x轴方向进入磁场Ⅱ,求场强度E的大小及方向;
(3)求第(2)问中电子离开磁场Ⅱ时的位置坐标.

(1)若电子离开磁场区域Ⅰ后直接进入第三象限,求入射速度的范围;
(2)若电子从(0,
| d |
| 2 |
(3)求第(2)问中电子离开磁场Ⅱ时的位置坐标.

(1)电子能从第三象限射出的临界轨迹如图甲所示.
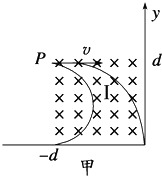
由几何知识可知,电子偏转半径范围为:
<r<d,
电子在匀强磁场中做匀速圆周运动,由牛顿第二定律得:evB=m
,
解得,电子入射速度的范围为:
<v<
.
(2)电子运动轨迹如图所示:

电子从(0,
)位置射出设电子在磁场中运动的轨道半径为R,由几何知识可得:
R2=(R-
)2+d2,
解得:R=
,
由牛顿第二定律得:evB=m
,
由几何关系得进入电场与水平方向的夹角为53°;
进入电场以后带电粒子垂直于x轴进入磁场Ⅱ,
知粒子在电场中做逆向平抛,根据平抛的规律:
带点粒子沿y轴方向的速度为:vy=v0sin53°=0.8v0,
带点粒子沿x轴方向的速度为:vx=v0cos53°=0.6v0,
根据位移的关系可以求得:E=
,方向沿x轴的正方向;
(3)根据粒子在电场中沿x轴运动规律:x=
at2,
则在磁场区域Ⅱ位置的横坐标为
d,
磁场区域Ⅱ,由牛顿第二定律得:evB=m
,
由几何知识可得:r=d,r2=(
d)2+y2,
解得:y=
d,
电子离开磁场Ⅱ时的位置坐标(d,-
d);
答:(1)入射速度的范围是:
<v<
;
(2)场强度E=
,方向沿x轴的正方向;
(3)电子离开磁场Ⅱ时的位置坐标是(d,-
d).

由几何知识可知,电子偏转半径范围为:
| d |
| 2 |
电子在匀强磁场中做匀速圆周运动,由牛顿第二定律得:evB=m
| v2 |
| r |
解得,电子入射速度的范围为:
| eBd |
| 2m |
| eBd |
| m |
(2)电子运动轨迹如图所示:

电子从(0,
| d |
| 2 |
R2=(R-
| d |
| 2 |
解得:R=
| 5d |
| 4 |
由牛顿第二定律得:evB=m
| ||
| R |
由几何关系得进入电场与水平方向的夹角为53°;
进入电场以后带电粒子垂直于x轴进入磁场Ⅱ,
知粒子在电场中做逆向平抛,根据平抛的规律:
带点粒子沿y轴方向的速度为:vy=v0sin53°=0.8v0,
带点粒子沿x轴方向的速度为:vx=v0cos53°=0.6v0,
根据位移的关系可以求得:E=
| 3edB2 |
| 2m |
(3)根据粒子在电场中沿x轴运动规律:x=
| 1 |
| 2 |
则在磁场区域Ⅱ位置的横坐标为
| 3 |
| 16 |
磁场区域Ⅱ,由牛顿第二定律得:evB=m
| v2 |
| r |
由几何知识可得:r=d,r2=(
| 3 |
| 16 |
解得:y=
| ||
| 16 |
电子离开磁场Ⅱ时的位置坐标(d,-
| ||
| 16 |
答:(1)入射速度的范围是:
| eBd |
| 2m |
| eBd |
| m |
(2)场强度E=
| 3edB2 |
| 2m |
(3)电子离开磁场Ⅱ时的位置坐标是(d,-
| ||
| 16 |

练习册系列答案
相关题目