题目内容
(18分)如图所示,在屏蔽装置底部中心位置O点放一医用放射源,可通过细缝沿扇形区域向外辐射速率为 的
的 粒子。已知屏蔽装置宽AB=9cm、缝长AD=18cm,
粒子。已知屏蔽装置宽AB=9cm、缝长AD=18cm, 粒子的质量
粒子的质量 ,电量
,电量 。若在屏蔽装置右侧条形区域内加一匀强磁场来隔离辐射,磁感应强度
。若在屏蔽装置右侧条形区域内加一匀强磁场来隔离辐射,磁感应强度 ,方向垂直于纸面向里,整个装置放于真空环境中。
,方向垂直于纸面向里,整个装置放于真空环境中。
(1)若所有的 粒子均不能从条形磁场隔离区的右侧穿出,则磁场的宽度d至少是多少?
粒子均不能从条形磁场隔离区的右侧穿出,则磁场的宽度d至少是多少?
(2)若条形磁场的宽度d=20cm,则射出屏蔽装置的 粒子在磁场中运动的最长时间和最短时间各是多少?(结果保留2位有效数字)
粒子在磁场中运动的最长时间和最短时间各是多少?(结果保留2位有效数字)
(1)0.34cm;(2) ;
; 。
。
解析试题分析:(1)由题意:AB=9cm,AD=18cm,可得: ①
①
所有α粒子在磁场中做匀速圆周运动的半径相同,设为R,根据牛顿第二定律有: ②
②
解得 R="0.2m=20cm" ③
由题意及几何关系可知:若条形磁场区域的右边界与沿OD方向进入磁场的α粒子的圆周轨迹相切,则所有α粒子均不能从条形磁场隔离区右侧穿出,如图一所示。设此时磁场宽度为d0,由几何关系: ④
④

(2)设α粒子在磁场内做匀速圆周运动的周期为T,则: ⑤
⑤
设速度方向垂直于AD进入磁场区域的α粒子的入射点为E,如图二所示,因磁场宽度d=20cm<d0,且R=20cm,则在∠EOD间岀射进入磁场区域的α粒子均能穿出磁场的右边界,在∠EOA间岀射进入磁场区域的α粒子均不能穿出磁场有边界,所以沿OE方向进入磁场区域的α粒子运动轨迹与磁场的右边界相切,在磁场中运动的时间最长。⑥
设在磁场中运动的最长时间为tmax,则: ⑦
⑦
若α粒子在磁场中做匀速圆周运动对应的圆弧轨迹的弦最短,则α粒子穿过磁场的时间最短,最短的弦长为磁场的宽度d0⑧
设再磁场中运动的最短时间为tmin,轨迹如图二所示,因R=d,则圆弧对应的圆心角为600,故: ⑨
⑨
考点:带电粒子在匀强磁场中的运动。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

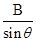

 、
、 为水平放置的间距
为水平放置的间距 的两块足够大的平行金属板,两板间有方向由
的两块足够大的平行金属板,两板间有方向由 。在
。在 ,油漆喷枪可向各个方向均匀地喷出初速度大小均为
,油漆喷枪可向各个方向均匀地喷出初速度大小均为 的油漆微粒,已知油漆微粒的质量均为
的油漆微粒,已知油漆微粒的质量均为 、电荷量均为
、电荷量均为 ,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度
,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度 。求:
。求:

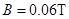 ,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变。
,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变。 的带电粒子以大小为 v 0的初速度自点
的带电粒子以大小为 v 0的初速度自点 沿+x 方向运动,恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终从 x轴上的点 Q(9 d,0 )沿-y 方向进入第Ⅳ象限;已知该匀强磁场的磁感应强度为
沿+x 方向运动,恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终从 x轴上的点 Q(9 d,0 )沿-y 方向进入第Ⅳ象限;已知该匀强磁场的磁感应强度为  ,不计粒子重力。
,不计粒子重力。 


 和
和 间的距离为
间的距离为 ,现在
,现在 =0时
=0时 ,反向值也为
,反向值也为 的带正电且电荷量为
的带正电且电荷量为 的粒子组成的粒子束,从
的粒子组成的粒子束,从 的中点
的中点 以平行于金属板方向
以平行于金属板方向 的速度
的速度 不断射入,所有粒子不会撞到金属板且在
不断射入,所有粒子不会撞到金属板且在 ,不计重力影响。试求:
,不计重力影响。试求:
 点的距离范围;
点的距离范围;