��Ŀ����
20�� ��ͼ��ʾ���ڴŸ�ǿ��ΪB������ֱֽ���������ǿ�ų��У���һ��ֱ���õĹ⻬������������������ֵΪR�ĵ��裬���ڹ���ϵĽ�����ab����ΪL������Ϊm������Ϊr����������ֱ��������ʹab���ع�����ٶ�v�����ϻ���������費�ƣ�ab��ʼ��ˮƽ���������뵼��ĽӴ����ã�����
��ͼ��ʾ���ڴŸ�ǿ��ΪB������ֱֽ���������ǿ�ų��У���һ��ֱ���õĹ⻬������������������ֵΪR�ĵ��裬���ڹ���ϵĽ�����ab����ΪL������Ϊm������Ϊr����������ֱ��������ʹab���ع�����ٶ�v�����ϻ���������費�ƣ�ab��ʼ��ˮƽ���������뵼��ĽӴ����ã�������1��ͨ������R�ĵ���������Σ�
��2������R���˵ĵ�ѹ�Ƕ��٣�
��3�������Ĺ����Ƕ��٣�
���� 1���������ֶ���֪��Ӧ��������
2�����ݽ������и�Ÿ��߲����ĸ�Ӧ�綯�ƿɼ������Ӧ������������ab�൱�ڵ�Դ��ab���˵ĵ�ѹ�൱�ڵ�Դ��·�˵�ѹ������Uab=IR��
3���Ӷ���ð����������ڽ������������˶���������ƽ�⣬��F=Mg+F���������������Ĺ��ʵĹ�ʽP=Fv��ֱ�Ӽ��㼴�ɣ�
��� �⣺��1���������ֶ���֪��Ӧ����ͨ��R�ķ������ң�
��2�������˲����ĸ�Ӧ�綯��Ϊ��E=BLv
����ŷķ���ɣ�ͨ�������˵ĵ���Ϊ��I=$\frac{E}{R+r}$
������ab�൱�ڵ�Դ��ab���˵ĵ�ѹ�൱�ڵ�Դ��·�˵�ѹ����R���˵ĵ�ѹ���У�
Uab=IR=$\frac{RBLv}{R+r}$
��3���������ֶ��������ܵ���������ֱ���£���СΪ��F=BId=BL$\frac{BLv}{R+r}$��
���ڽ�����������ֱ���˶�������ƽ�������У�F=Mg+F����
��ã�F=Mg+$\frac{{B}^{2}{L}^{2}v}{R+r}$
�����Ĺ���Ϊ��P=Fv=��Mg+$\frac{{B}^{2}{L}^{2}v}{R+r}$��v
�𣺣�1��ͨ������R�ĵ����������ң�
��2������R���˵ĵ�ѹ��$\frac{RBLv}{R+r}$��
��3�������Ĺ����ǣ�Mg+$\frac{{B}^{2}{L}^{2}v}{R+r}$��v��
���� �����ǵ�Ÿ�Ӧ�еĶ���ѧ����͵�·������ۺ��⣬�ؼ�Ҫ������������˵������������һ�����Ѷȣ������е���

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д� ��ͼ��ʾ����ƽ�н�������ֱ���ã�����A��B��������ˮƽ��ԣ�����ѹΪ500V��һ������Ϊ400eV�Ĵ������ӵ������СΪe����A���ش�ֱ�巽������糡�У�����һ��ʱ�������뿪�糡���������뿪�糡ʱ�Ķ��ܴ�С����Ϊ��������
��ͼ��ʾ����ƽ�н�������ֱ���ã�����A��B��������ˮƽ��ԣ�����ѹΪ500V��һ������Ϊ400eV�Ĵ������ӵ������СΪe����A���ش�ֱ�巽������糡�У�����һ��ʱ�������뿪�糡���������뿪�糡ʱ�Ķ��ܴ�С����Ϊ��������| A�� | 900eV | B�� | 500eV | C�� | 400eV | D�� | 100eV |
 ����ͼ��ʾ�ĵ�·�У������ѹ���ij�����Ȧ�ϼ�һ����Чֵ����Ľ�����ѹ������S���ڶϿ�״̬����ô������˵������ȷ���ǣ�������
����ͼ��ʾ�ĵ�·�У������ѹ���ij�����Ȧ�ϼ�һ����Чֵ����Ľ�����ѹ������S���ڶϿ�״̬����ô������˵������ȷ���ǣ�������| A�� | ������������R1�Ļ�����ͷP�����ƶ�ʱ������L������ | |
| B�� | ������������R1�Ļ�����ͷP�����ƶ�ʱ��������A1�Ķ�������� | |
| C�� | ���պϿ���S���������A1�Ķ������ѹ��V�Ķ������� | |
| D�� | ���պϿ���S���������A1�Ķ�����С����������A2�Ķ������� |
A���ɵ�أ����⣩
B����ֵ����R1=480��
C������������R2��0��15����
D��������A1 ������0.3��������0.6A��
E��������A2 ������0.1��������3A��
F��������A3 ������20��������300mA��
G��������A4 ������20��������3mA��
H������K
J����������
Ϊ�˷��㡢ȷ�ز����Դ�綯�ƺ��ڵ��裮

�ٵ�·ͼ��a��������Ӧѡ��A4��b��������Ӧѡ��A1��
�ڱ���ij��ʵ���в���������ݣ�����ͼ2�л���Ia-Ibͼ��
| 1 | 2 | 3 | 4 | 5 | |
| Ia��mA�� | 2.80 | 2.60 | 2.50 | 2.20 | 2.00 |
| Ib��A�� | 0.12 | 0.24 | 0.27 | 0.45 | 0.57 |
 ����Ϊm�����徲ֹ�ڹ⻬ˮƽ���ϣ���t=0ʱ�̿�ʼ�ܵ�ˮƽ�������ã����Ĵ�СF��ʱ��t�Ĺ�ϵ��ͼ��ʾ�����ķ��ֲ��䣬������˵����ȷ���ǣ�������
����Ϊm�����徲ֹ�ڹ⻬ˮƽ���ϣ���t=0ʱ�̿�ʼ�ܵ�ˮƽ�������ã����Ĵ�СF��ʱ��t�Ĺ�ϵ��ͼ��ʾ�����ķ��ֲ��䣬������˵����ȷ���ǣ�������| A�� | 2t0ʱ�̵�˲ʱ�ٶ�Ϊ$\frac{6{F}_{0}{t}_{0}}{m}$ | |
| B�� | ��t=t0��2t0���ʱ�������巢����λ��$\frac{5{F}_{0}{{t}_{0}}^{2}}{2m}$ | |
| C�� | 3t0ʱ�̵�˲ʱ����Ϊ$\frac{12{{F}_{0}}^{2}{t}_{0}}{m}$ | |
| D�� | ��t=0��3t0���ʱ���ڣ�ˮƽ����ƽ������Ϊ$\frac{9{{F}_{0}}^{2}{t}_{0}}{m}$ |
 ��ͼ��ʾ���ڵ綯���������£�Ƥ��������Ϸ���Ƥ���Խ�һ��������С���ƣ���Ƥ�����A��������£�A�㵽Ƥ���Ҷ�Ի�˾���Ϊ��s����������Ƥ����Ķ�Ħ������Ϊ�̣�����B���ʱ��ֵ����Ϊ��������
��ͼ��ʾ���ڵ綯���������£�Ƥ��������Ϸ���Ƥ���Խ�һ��������С���ƣ���Ƥ�����A��������£�A�㵽Ƥ���Ҷ�Ի�˾���Ϊ��s����������Ƥ����Ķ�Ħ������Ϊ�̣�����B���ʱ��ֵ����Ϊ��������| A�� | $\frac{S}{v}$ | B�� | $\frac{2S}{v}$ | C�� | $\frac{S}{v}$+$\frac{v}{2��g}$ | D�� | $\sqrt{\frac{2S}{��g}}$ |

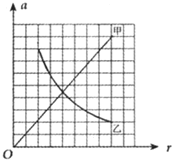 �ס�������������Բ���˶������ļ��ٶ�a ��뾶r�仯�Ĺ�ϵ��ͼ��ʾ����Ϊһ��бֱ�ߣ���Ϊ˫���ߵ�һ���֣�������4��˵����
�ס�������������Բ���˶������ļ��ٶ�a ��뾶r�仯�Ĺ�ϵ��ͼ��ʾ����Ϊһ��бֱ�ߣ���Ϊ˫���ߵ�һ���֣�������4��˵���� ��ͼ1��ʾ����һ�������ڣ�һ��鱻һ���ʵ��ɽ�ѹ���컨���ϣ����ɵ��¶˹̶����������ĵذ��ϣ����ɱ�����ֱ�������������й����У����δ���뿪���������컨�壮������������ͼ2��ʾ��v-tͼ������ʱ����֪�������컨������ѹ��F1�͵ذ�����ѹ��F2��ʱ��仯�Ķ���ͼ�������ȷ���ǣ�������
��ͼ1��ʾ����һ�������ڣ�һ��鱻һ���ʵ��ɽ�ѹ���컨���ϣ����ɵ��¶˹̶����������ĵذ��ϣ����ɱ�����ֱ�������������й����У����δ���뿪���������컨�壮������������ͼ2��ʾ��v-tͼ������ʱ����֪�������컨������ѹ��F1�͵ذ�����ѹ��F2��ʱ��仯�Ķ���ͼ�������ȷ���ǣ�������


