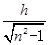题目内容
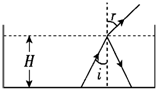
如图所示是一透明的圆柱体的横截面，半径R=2cm，折射率n=
．真空中一束光线沿平行于直径AB的方向从D点射人透明体，折射光线恰好通过B点．真空中光速c=3.0×108m/s，求：
①光在透明体中的传播速度v．
②入射点D与AB间的距离d．
| 3 |
①光在透明体中的传播速度v．
②入射点D与AB间的距离d．
①光在透明体中的传播速度v=
=
m/s=1.73×108m/s
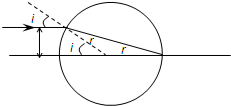
②光线PC经折射后经过B点后光路图如图所示．
由折射定律得 n=
，
又由几何关系得：i=2r，
代入解得：i=60°
所以光线偏离直线AB的距离d=Rsini=2×sin60°=1.73cm
答：
①光在透明体中的传播速度v为1.73×108m/s．
②入射点D与AB间的距离d为1.73cm．
| c |
| n |
| 3.0×108 | ||
|
②光线PC经折射后经过B点后光路图如图所示．
由折射定律得 n=
| sini |
| sinr |
又由几何关系得：i=2r，
代入解得：i=60°
所以光线偏离直线AB的距离d=Rsini=2×sin60°=1.73cm
答：
①光在透明体中的传播速度v为1.73×108m/s．
②入射点D与AB间的距离d为1.73cm．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
