题目内容
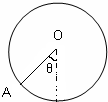 半径R=0.4m的光滑绝缘轨道固定于竖直于平面内,加上某一方向的匀强电场时,带电小球沿轨道内侧做圆周运动,小球动能最大位置在A点,圆心O与A点的连线与竖直线成一角度θ,如图所示,在A点时小球对轨道压力N=108N,若小球的最大动能比最小动能多14.4J,且小球能够到达轨道上任意一点(不计空气阻力),试求:
半径R=0.4m的光滑绝缘轨道固定于竖直于平面内,加上某一方向的匀强电场时,带电小球沿轨道内侧做圆周运动,小球动能最大位置在A点,圆心O与A点的连线与竖直线成一角度θ,如图所示,在A点时小球对轨道压力N=108N,若小球的最大动能比最小动能多14.4J,且小球能够到达轨道上任意一点(不计空气阻力),试求:(1)小球的最小动能;
(2)若小球在动能最小位置时突然撤去轨道,并保持其他量都不变,则小球经0.02s时,其动能与在A点时的动能相等,小球的质量为多少?
分析:(1)带电小球沿轨道内侧做圆周运动,受到重力和电场力作用,其合力是恒力,当合力沿OA连线向下时,小球通过A点时动能最大,通过关于O点对称的B点时动能最小.根据动能定理研究小球从B运动到A点的过程,求出重力与电场力的合力大小.根据牛顿第二定律和动能的计算式求出A点的动能,再求出小球的最小动能;
(2)在B点撤去轨道后,小球将做类平抛运动,由题,小球经0.02s时,其动能与在A点时的动能相等,说明小球经0.02s时偏转量等于2R,由位移公式和牛顿第二定律结合求出质量.
(2)在B点撤去轨道后,小球将做类平抛运动,由题,小球经0.02s时,其动能与在A点时的动能相等,说明小球经0.02s时偏转量等于2R,由位移公式和牛顿第二定律结合求出质量.
解答:解:据题分析可知,小球的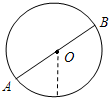 重力与电场力的合力方向必沿OA连线向下,最小动能的位置必在A点关于O点对称的B点
重力与电场力的合力方向必沿OA连线向下,最小动能的位置必在A点关于O点对称的B点
则有
F?2R=
mvA2-
mvB2
代入解得F=18N
在A点时有 N-F=m
mvA2=
(N-F)=18J
所以最小动能为Ekm=
mvB2=18J-14.4J=3.6J
②在B点撤去轨道后,小球将做类平抛运动
由2R=
at2,F=ma得
m=
=4.5×10-3kg
答:
(1)小球的最小动能是3.6J;
(2)小球的质量为4.5×10-3kg.
 重力与电场力的合力方向必沿OA连线向下,最小动能的位置必在A点关于O点对称的B点
重力与电场力的合力方向必沿OA连线向下,最小动能的位置必在A点关于O点对称的B点则有
F?2R=
| 1 |
| 2 |
| 1 |
| 2 |
代入解得F=18N
在A点时有 N-F=m
| νA2 |
| R |
| 1 |
| 2 |
| R |
| 2 |
所以最小动能为Ekm=
| 1 |
| 2 |
②在B点撤去轨道后,小球将做类平抛运动
由2R=
| 1 |
| 2 |
m=
| Ft2 |
| 4R |
答:
(1)小球的最小动能是3.6J;
(2)小球的质量为4.5×10-3kg.
点评:本题可以运用竖直平面内绳子系住的小球运动进行类比,A相当于物理的最低点,B相当于物理的最高点.

练习册系列答案
相关题目
 (2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(2010?南平模拟)如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则: 如图所示,距水平地面高为h=0.4m处,水平固定一根长直光滑杆,杆上P点固定一可绕水平轴无摩擦转动且不计大小的定滑轮,一半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,杆和半圆形轨道在同一竖直面内,杆上套有一质量m=2kg小球A,半圆形轨道上套有一质量也为m=2kg的小球B,两球用一条不可伸长的轻绳通过定滑轮连接,且均可看作质点,现给小球A施加一个水平向右的恒力F=55N,g取10m/s2.求:
如图所示,距水平地面高为h=0.4m处,水平固定一根长直光滑杆,杆上P点固定一可绕水平轴无摩擦转动且不计大小的定滑轮,一半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,杆和半圆形轨道在同一竖直面内,杆上套有一质量m=2kg小球A,半圆形轨道上套有一质量也为m=2kg的小球B,两球用一条不可伸长的轻绳通过定滑轮连接,且均可看作质点,现给小球A施加一个水平向右的恒力F=55N,g取10m/s2.求: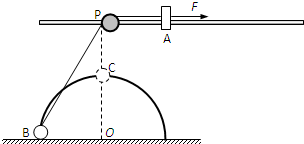 (2011?上海模拟)如图所示,在距水平地面高为H=0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则:
(2011?上海模拟)如图所示,在距水平地面高为H=0.4m处,水平固定一根长直光滑杆,杆上P处固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套一质量m=3kg的滑块A.半径R=0.3m的光滑半圆形轨道竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量m=3kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,滑块和小球均可看作质点,且不计滑轮大小的影响.现给滑块A施加一个水平向右、大小为60N的恒力F,则: 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2.现给小球A一个水平向右的恒力F=55N.求:(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;(2)小球B运动到C处时的速度大小;(3)小球B被拉到离地多高时与小球A速度大小相等.
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取10m/s2.现给小球A一个水平向右的恒力F=55N.求:(1)把小球B从地面拉到P点正下方C点过程中,力F做的功;(2)小球B运动到C处时的速度大小;(3)小球B被拉到离地多高时与小球A速度大小相等. 如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取
如图所示,在距水平地面高为0.4m处,水平固定一根长直光滑杆,在杆上P点固定一定滑轮,滑轮可绕水平轴无摩擦转动,在P点的右边,杆上套有一质量m=2kg小球A.半径R=0.3m的光滑半圆形细轨道,竖直地固定在地面上,其圆心O在P点的正下方,在轨道上套有一质量也为m=2kg的小球B.用一条不可伸长的柔软细绳,通过定滑轮将两小球连接起来.杆和半圆形轨道在同一竖直面内,两小球均可看作质点,且不计滑轮大小的影响,g取