题目内容
一辆质量m=2.0×103kg的汽车,经过半径r=50m的水平弯路.则:
(1)当汽车的速率v=10m/s时,需要的向心力为多大?
(2)若汽车轮胎与路面间的最大静摩擦力Fm=1.2×104N,为了使这辆车通过此段弯路时不发生侧滑,行驶速率的极限为多大?
(3)试分析,在F1方程式赛车中,如果仅从安全角度考虑,转弯时赛车手应选择内侧车道还是外侧车道?
(1)当汽车的速率v=10m/s时,需要的向心力为多大?
(2)若汽车轮胎与路面间的最大静摩擦力Fm=1.2×104N,为了使这辆车通过此段弯路时不发生侧滑,行驶速率的极限为多大?
(3)试分析,在F1方程式赛车中,如果仅从安全角度考虑,转弯时赛车手应选择内侧车道还是外侧车道?
(1)汽车做匀速圆周运动,向心力为:
Fn=m
=2.0×103×
=4.0×103N;
(2)汽车做匀速圆周运动,静摩擦力提供向心力,当静摩擦力达到最大时,汽车的速度达到最大,根据牛顿第二定律,有:
Fm=m
解得:
vm=
=
=10
m/s;
(3)在F1方程式赛车中,如果仅从安全角度考虑,根据公式Fn=m
,转弯半径越大,需要的向心力越小,越安全,故要在外侧车道转弯;
答:(1)当汽车的速率v=10m/s时,需要的向心力为4.0×103N;
(2)行驶速率的极限为10
m/s;
(3)在F1方程式赛车中,如果仅从安全角度考虑,转弯时赛车手应选择外侧车道.
Fn=m
| v2 |
| r |
| 102 |
| 50 |
(2)汽车做匀速圆周运动,静摩擦力提供向心力,当静摩擦力达到最大时,汽车的速度达到最大,根据牛顿第二定律,有:
Fm=m
| vm2 |
| r |
解得:
vm=
|
|
| 3 |
(3)在F1方程式赛车中,如果仅从安全角度考虑,根据公式Fn=m
| v2 |
| r |
答:(1)当汽车的速率v=10m/s时,需要的向心力为4.0×103N;
(2)行驶速率的极限为10
| 3 |
(3)在F1方程式赛车中,如果仅从安全角度考虑,转弯时赛车手应选择外侧车道.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目

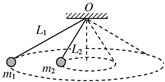
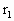 =20cm,B离轴心
=20cm,B离轴心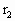 =30cm,A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍.求:
=30cm,A、B与盘面间相互作用的最大静摩擦力为其重力的0.4倍.求: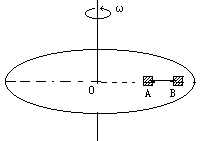
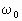 =?
=?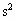 )
)