题目内容
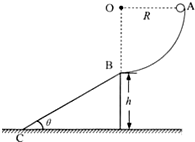
如图所示,在竖直平面内有一半径R=5m的四分之一粗糙圆弧轨道与一倾角为θ=37°的斜面相连,现有一质量m=0.9kg的小球(可视为质点),从圆弧轨道顶端A点由静止滑下,至轨道底端B点时水平飞出,最后刚好落到斜面底端C处,已知斜面顶端至地面高h=5m,取g=10m/s2、sin37.=0.6,cos37°=0.8.求:
(1)小球对圆弧轨道底端B点的压力
(2)小球从圆弧轨道顶端A点滑到底端B点过程中克服摩擦力做的功.
(1)小球对圆弧轨道底端B点的压力
(2)小球从圆弧轨道顶端A点滑到底端B点过程中克服摩擦力做的功.

(1)设小球从圆弧轨道底端B点水平滑出后以v0的水平初速做平抛运动,位移为x,则有:
x=v0t…①
h=
gt2…②
tanθ=
=
…③
设小球在圆弧轨道底端B点受到支持力为FN,根据牛顿第二定律得:
FN-mg=m
…④
根据牛顿第三定律,小球对圆弧轨道底端B点的压力为:FN′=FN
联立以上各式,代入数据得:FN′=17N…⑤
(2)设小球从圆弧轨道顶端A点滑到B点过程中克服摩擦力做的功为Wf,由动能定理有:
mgR-Wf=
mv02…⑥
代入数据解得:Wf=25J…⑦
答:(1)小球对圆弧轨道底端B点的压力为17N;
(2)小球从圆弧轨道顶端A点滑到底端B点过程中克服摩擦力做的功为25J.
x=v0t…①
h=
| 1 |
| 2 |
tanθ=
| h |
| x |
| gt |
| 2v0 |
设小球在圆弧轨道底端B点受到支持力为FN,根据牛顿第二定律得:
FN-mg=m
| v02 |
| R |
根据牛顿第三定律,小球对圆弧轨道底端B点的压力为:FN′=FN
联立以上各式,代入数据得:FN′=17N…⑤
(2)设小球从圆弧轨道顶端A点滑到B点过程中克服摩擦力做的功为Wf,由动能定理有:
mgR-Wf=
| 1 |
| 2 |
代入数据解得:Wf=25J…⑦
答:(1)小球对圆弧轨道底端B点的压力为17N;
(2)小球从圆弧轨道顶端A点滑到底端B点过程中克服摩擦力做的功为25J.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目