Question

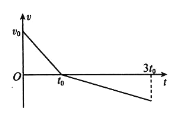
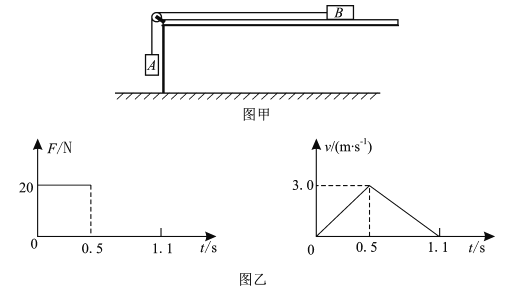
【题目】重物A和滑块B用轻细线跨过光滑定滑轮相连，A距地面一定高度，B可在水平轻细线牵引下在水平足够长的粗糙木板上滑动，重物A运动一段距离后将落在地面上不再运动，如图甲所示。从某时刻起释放滑块B，测得滑块B所受细线拉力F随时间t变化的图象和滑块B的v—t图象，如图乙所示，不计空气阻力，g=10m/s2。

（1）求刚释放滑块B时，重物A距地面的高度；

（2）求重物A的质量及重物B与木板间的动摩擦因数；

（3）已知重物B的质量mB=kg，若重物A的质量变为10kg，其它条件不变，从某时刻起释放滑块B，求滑块B运动的最大距离（保留一位小数）。

Answer 1

【答案】（1）0.75m；（2）0.5；（3）1.9m

【解析】

（1）由图像可知，在绳子对B有拉力，然后就没有拉力了，说明时刻重物A正好落地，说明这段时间内B的位移正好等于A下落的高度即重物A距离地面的高度，由v-t图象可得，刚释放滑块B时，重物A距地面的高度

（2）设重物A的质量为mA，重物A做匀加速运动的加速度为a1，由牛顿第二定律得

mA g－F=mA a1

由v-t图象和F-t图象可得

F=20N

解得

滑块B做匀减速运动的加速度的大小

设滑块B的质量为，由牛顿第二定律得

解得动摩擦因数

（3）若重物A的质量变为mA′=10kg时，设其加速度为a1′，轻绳拉力为F′，对重物A、B，分别由牛顿第二定律得

设滑块B运动的最大速度为vm，减速运动的位移为x，由运动学公式得

解得

滑块B运动的最大距离为