题目内容
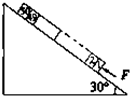
如图,粗糙的斜坡倾角为30.,有一物体从点A以某一初速度开始向上运动,经过2s到达点B速度恰好为零,然后又从点B返回到点A,已知点A、B间距离为l6m,则从点B由静止返回点A所需的时间为( )

| A.3s | B.4s | C.5s | D.6s |

上升过程中的平均速度
=
=
m/s=8m/s
所以上升时的加速度a1=
=
m/s=8m/s2
根据牛顿第二定律得:
上升时:mgsinα+f=ma1
下滑时:mgsinα-f=ma2
解得:a2=2m/s2
从B点返回的时间:t1=
=
s=4s
故选:B
| . |
| v |
| x |
| t |
| 16 |
| 2 |
所以上升时的加速度a1=
| △v | ||
|
| 8 |
| 1 |
根据牛顿第二定律得:
上升时:mgsinα+f=ma1
下滑时:mgsinα-f=ma2
解得:a2=2m/s2
从B点返回的时间:t1=
|
|
故选:B

练习册系列答案
相关题目