题目内容
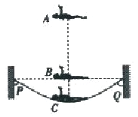
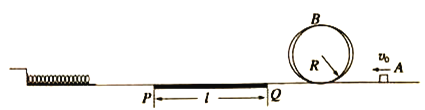
【题目】如图所示，在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道，水平轨道的PQ段长度为l=2.5m，上面铺设特殊材料，小物块与其动摩擦因数为μ=0.3，轨道其它部分摩擦不计。水平轨道左侧有一轻质弹簧左端固定，弹簧处于原长状态。可视为质点的质量m=1kg的小物块从轨道右侧A点以初速度
冲上轨道，通过圆形轨道，水平轨道后压缩弹簧，并被弹簧以原速率弹回，取
，求：
（1）弹簧获得的最大弹性势能
；
（2）小物块被弹簧第一次弹回经过圆轨道最低点时的动能
；
（3）当R满足什么条件时，小物块被弹簧第一次弹回圆轨道时能沿轨道运动而不会脱离轨道。
【答案】（1）10.5J （2）3J （3）①
，②
或
【解析】(1)当弹簧被压缩到最短时，其弹性势能最大。
从A到压缩弹簧至最短的过程中，由动能定理
由功能关系：
，
解得:
；
(2)小物块从开始运动到第一次被弹回圆形轨道最低点的过程中，由动能定理
解得
；
(3)小物块第一次返回后进入圆形轨道的运动，有以下两种情况：
①小球能够绕圆轨道做完整的圆周运动，此时设小球最高点速度为
，由动能定理
小物块能够经过最高点的条件
，解得
②小物块不能够绕圆轨道做圆周运动，为了不让其脱离轨道，小物块至多只能到达与圆心等高的位置，即
，解得
；
设第一次自A点经过圆形轨道最高点时，速度为
，
由动能定理：
且需要满足，
解得
，
综合以上考虑，R需要满足的条件为：或
练习册系列答案
相关题目
