题目内容
【题目】如图所示,一截面为直角三角形的玻璃棱镜ABC,∠A=30°,D点是AC的中点,AD间距为L。一条光线从D点沿平行于AB方向射入棱镜,光线垂直BC从F点(图中未画出)射出。已知真空中光速为C,求:
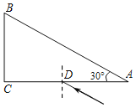
(ⅰ)玻璃的折射率n;
(ⅱ)光在介质中从D点到F点经过的时间t。
【答案】(1)![]() (2)
(2)![]()
【解析】
(ⅰ)光路图如图所示,
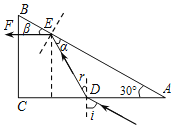
设在AC面入射角为i,折射角为r,在AB面,光线与AB的夹角为α,反射光线与AB的夹角为β,光线垂直BC射出,由几何知识可得:α=β=30°,i=60°,α+r=60°,r=30°
折射率![]()
解得: ![]()
(ⅱ)由于α=∠A,所以△ADE为等腰三角形,则有:DE=AD=L,DC=EF+DE cos(90°-r)
设光线从D点到F点经过的距离为x,光线在玻璃中传播速度为v,传播时间为t,则:x=DE+EF
![]()
![]()
解得:![]()

练习册系列答案
相关题目