Question

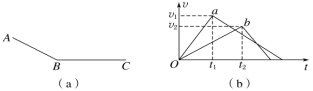
【题目】如图所示，AB、CD为两个光滑的平台，一倾角为37°，长为5 m的传送带与两平台平滑连接。现有一小物体以10 m/s的速度沿AB平台向右运动，当传送带静止时，小物体恰好能滑到CD平台上，问：

(1)小物体跟传送带间的动摩擦因数多大？

(2)当小物体在AB平台上的运动速度低于某一数值时，无论传送带顺时针运动的速度多大，小物体总不能到达平台CD，求这个临界速度。

(3)若小物体以8 m/s的速度沿平台AB向右运动，欲使小物体到达平台CD，传送带至少以多大的速度顺时针运动？

Answer 1

【答案】 (1)0.5 (2)2 m/s (3)3 m/s

【解析】 (1)传送带静止时，小物体在传送带上受力如图甲所示，

据牛顿第二定律得：μmgcos θ＋mgsin θ＝ma1 ①

B→C过程有：v02＝2a1l ②

解得：a1＝10 m/s2，μ＝0.5。

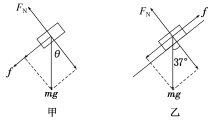
(2)显然，当小物体受到的摩擦力始终向上时，最容易到达传送带顶端，此时，小物体受力如图乙所示，据牛顿第二定律得：

mgsin 37°－μmgcos 37°＝ma2 ③

若恰好能到达高台时，有：v2＝2a2l ④

解得：v＝2 m/s

即当小物体在AB平台上向右滑动速度小于2 m/s时，无论传送带顺时针传动的速度多大，小物体总不能到达平台CD。

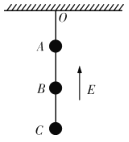
(3)以v1表示小物体在平台AB上的滑动速度，

以v2表示传送带顺时针传动的速度大小，

对从小物体滑上传送带到小物体速度减小到传送带速度过程有：

v12－v22＝2a1x1 ⑤

对从小物体速度减小到带速v2开始，到运动到恰滑上CD平台过程，有：

v22＝2a2x2 ⑥

x1＋x2＝L ⑦

解得：v2＝3 m/s

即传送带至少以3 m/s的速度顺时针运动，小物体才能到达平台CD。