题目内容
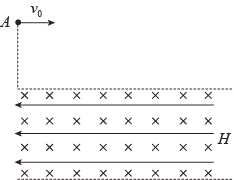
【题目】如图所示，在竖直平面内xOy坐标系中分布着与水平方向夹45°角的匀强电场，将一质量为m，带电量为q的小球，以某一初速度从O点竖直向上抛出，它的运动轨迹恰好满足抛物线方程y=kx2，小球运动能通过P（
，）.已知重力加速度为g，求：
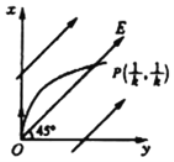
（1）该匀强电场的电场强度E=？
（2）小球到达P点所用时间t及末动能Ek.
【答案】(1)E=
(2)Ek=
【解析】
（1）小球以某一初速度从O点竖直向上抛出，它的轨迹恰好满足抛物线方程为y=kx2，说明小球做类平抛运动，则电场力与重力的合力沿y轴正方向；
竖直方向受力平衡：qEsin45°=mg，
解得电场强度的大小为E=
；
（2）小球受到的合力：F合=qEcos45°=mg=ma，所以a=g，
由平抛运动规律有：y方向：
=
gt2，
解得t=
；
竖直方向：=v0t，
解得初速度大小为v0=
；
根据动能定理可得ma
=Ek-
解得：Ek=
练习册系列答案
相关题目
