题目内容
3．
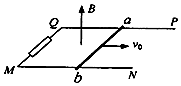如图所示，光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中，磁感应强度为B，导轨宽度为L．QM之间接有阻值为R的电阻，其余部分电阻不计．一质量为m，电阻为R的金属棒ab放在导轨上，给棒一个水平向右的初速度v0使之开始滑行，最后停在导轨上．由以上条件，在此过程中不能求出的物理量有（ ）| A． | 电阻R上产生的焦耳热 | B． | ab棒运动的时间 | ||
| C． | 通过电阻R的总电荷量 | D． | ab棒运动的位移 |
分析 明确导体棒的运动过程，分析其受力和能量转化关系，知道停止运动时其动能全部转化为内能，即可由能量守恒求出焦耳热；根据动量定理列式求电荷量；根据感应电荷量q=$\frac{△Φ}{R}$可求出电量．但由于加速度变化，故时间无法求出．
解答 解：A、根据能量守恒得：电阻R上产生的焦耳热Q=frac12mv02，
B、由于ab棒做变减速运动，无法求出时间，
C、根据动量定理得：-B$\overline{I}$L△t=0-mv0，又q=$\overline{I}$△t，感应电荷量：q=$\frac{m{v}_{0}}{BL}$，
D、设ab棒运动的位移为s．感应电荷量q=$\frac{△Φ}{R}$=$\frac{BLS}{R}$，解得s=$\frac{qR}{BL}$，
本题选择无法求出的，故选：B．
点评 本题考查电磁感应与电路和能量关系结合的题目，由能量守恒可以求出电阻产生的焦耳热，同时注意电量可以根据法拉第电磁感应定律求出，但由于导体棒做加速度减小的减速运动，无法求出导体棒的运动时间．
练习册系列答案
相关题目
16．一个质量为0.18kg的垒球，以25m/s的水平速度飞向球棒，被球棒打击后，反向飞回，速度大小为45m/s．若球棒与垒球的作用时间为0.01s，下列说法正确的是（ ）
| A． | 球棒对垒球的平均作用力大小为360N | |
| B． | 球棒对垒球的平均作用力大小为1260N | |
| C． | 球棒对垒球的作用力大于垒球对球棒的作用力 | |
| D． | 如果延长球棒与垒球的作用时间，则垒球一定会获得更大的反向速度 |
12．
如图，电路中定值电阻阻值R大于电源内阻阻值r．将滑动变阻器滑片向下滑动，理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3，理想电流表Α示数变化量的绝对值为△I，则（ ）
如图，电路中定值电阻阻值R大于电源内阻阻值r．将滑动变阻器滑片向下滑动，理想电压表V1、V2、V3示数变化量的绝对值分别为△U1、△U2、△U3，理想电流表Α示数变化量的绝对值为△I，则（ ）| A． | A的示数减小 | B． | △U1小于△U2 | ||
| C． | △U3与△I的比值大于R+r | D． | 电源的输出功率一定增大 |
7．
一个人在岸上以恒定的速度v通过定滑轮收拢连接在船上的牵引绳．当船运动到如图所示位置时，绳子与水平方向的夹角为α，则船的运动速度为（ ）
一个人在岸上以恒定的速度v通过定滑轮收拢连接在船上的牵引绳．当船运动到如图所示位置时，绳子与水平方向的夹角为α，则船的运动速度为（ ）| A． | v | B． | vcosα | C． | $\frac{v}{cosα}$ | D． | vtanα |
14．关于单摆，下列说法中正确的是（ ）
| A． | 单摆在周期性外力作用下做受迫振动，其振动周期与单摆的摆长无关 | |
| B． | 摆角从5°改为3°，单摆的周期会变小 | |
| C． | 用等大的铜球替代铁球，单摆的周期不变 | |
| D． | 将单摆从赤道移到北极，单摆的周期会变大 |
11．如图甲所示，轻弹簧竖直固定在水平面上处于自由状态，一质量为m=0.2kg的小球，从弹簧上端某高度处自由下落，从它接触弹簧到弹簧压缩至最短的过程中（弹簧在弹性限度内），其速度u和弹簧压缩量△x之间的函数图象如图乙所示，其中A为曲线的最高点，小球和弹簧接触瞬间机械能损失不计，取g=10m/s2，则（ ）
| A． | 当△x=0.1m时，小球处于失重状态 | |
| B． | 小球在最低点时的加速度大于10m/s2 | |
| C． | 从接触弹簧到压缩至最短的过程中，小球的机械能守恒 | |
| D． | 小球从速度最大到压缩至最短，弹簧弹性势能增加量为3.621J |