题目内容
18.如图为实验室常用的气垫导轨验证动量守恒实验的装置,两带有等宽遮光条的滑块A和B,质量分别为mA、mB,在A、B间用细线水平压住一轻弹簧,将其置于气垫导轨上,调节导轨使其能实现处于静止状态,表明此时导轨处于水平.烧断细线,滑块A、B被弹簧弹开,相距足够远的光电门C、D记录下两遮光条通过的时间分别为tA和tB,若满足关系式$\frac{{m}_{A}}{{t}_{A}}$=$\frac{{m}_{B}}{{t}_{B}}$,则说明两滑块组成的系统动量守恒.在滑块A、B通过光电门时它们的动能之比为$\frac{{m}_{B}}{{m}_{A}}$.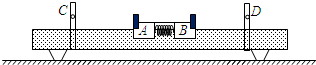
分析 滑块静止,处于平衡状态,所受合力为零,据此分析答题;求出滑块速度,由动量守恒定律分析答题;分别表示出动能表达式,联立动量守恒的结论式即可求得动能之比.
解答 解:两滑块自由静止,滑块静止,处于平衡状态,所受合力为零,此时气垫导轨是水平的;
设遮光条的宽度为d,两滑块的速度为:vA=$\frac{d}{{t}_{A}}$,vB=$\frac{d}{{t}_{B}}$…①,
如果动量守恒,设向右为正方向,则一定满足:mAvA-mBvB=0…②,
由①②解得:$\frac{{m}_{A}}{{t}_{A}}$=$\frac{{m}_{B}}{{t}_{B}}$ ③
两物体通过光电门时的动能之比为:
$\frac{{E}_{A}}{{E}_{B}}$=$\frac{{m}_{A}{v}_{A}^{2}}{{m}_{B}{v}_{B}^{2}}$=$\frac{{m}_{A}(\frac{d}{{t}_{A}})^{2}}{{m}_{B}(\frac{d}{{t}_{B}})^{2}}$=$\frac{{m}_{B}}{{m}_{A}}$
故答案为:气垫导轨水平;$\frac{{m}_{A}}{{t}_{A}}$=$\frac{{m}_{B}}{{t}_{B}}$.$\frac{{m}_{B}}{{m}_{A}}$
点评 本题考查了实验注意事项、实验数据处理,应用速度公式、动量守恒定律即可正确解题,要注意动量守恒定律的矢量性.

练习册系列答案
相关题目
11.关于近代物理内容的若干叙述,下列说法正确的是( )
| A. | 普朗克引入能量子的概念,得出黑体辐射的强度按波长分布的公式,与实验符合得非常好,并由此开创了物理学的新纪元 | |
| B. | 汤姆逊通过α粒子散射实验,提出了原子具有核式结构 | |
| C. | 根据爱因斯坦的光电效应理论,一束光照射到某种金属上不能发生光电效应,改用波长较长的光照射该金属可能发生 | |
| D. | 根据波尔理论,氢原子放出一个光子,其核外电子的运动半径增大 |
11.一颗子弹水平射入静止在光滑水平地面上的木块后不再穿出,木块的动能增加了20J,已知木块的质量小于子弹的质量,则此过程中产生的内能可能是( )
| A. | 18J | B. | 24J | C. | 32J | D. | 48J |
8.在生产车间的流水线上,用一个倾斜的传送带将工件由较低的工位传送到较高工位,传送带保持恒定的速度运动,将工件由静止放在传送带较低的一端,到达下一个工位之前,工件的速度与传送带的速度相同,在这一过程中,以下说法正确的是( )
| A. | 传送带与工件之间的摩擦力对工件做正功 | |
| B. | 传送带与工件之间的摩擦力对工件不做功 | |
| C. | 传送带的倾斜角度越大,工件与传送带之间的滑动摩擦力越小 | |
| D. | 工件的速度与传送带的速度相同后,工件所受摩擦力做功的功率为零 |
14.跳高比赛中,必须在运动员着地处铺上很厚的海绵垫子,这是为了( )
| A. | 减小运动员着地过程中受到的冲量作用 | |
| B. | 减小运动员着地过程中受到的平均冲力 | |
| C. | 减小运动员着地过程中动量的变化量 | |
| D. | 减小运动员的惯性 |
3.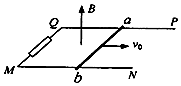 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中不能求出的物理量有( )
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中不能求出的物理量有( )
 如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中不能求出的物理量有( )
如图所示,光滑U型金属导轨PQMN水平固定在竖直向上的匀强磁场中,磁感应强度为B,导轨宽度为L.QM之间接有阻值为R的电阻,其余部分电阻不计.一质量为m,电阻为R的金属棒ab放在导轨上,给棒一个水平向右的初速度v0使之开始滑行,最后停在导轨上.由以上条件,在此过程中不能求出的物理量有( )| A. | 电阻R上产生的焦耳热 | B. | ab棒运动的时间 | ||
| C. | 通过电阻R的总电荷量 | D. | ab棒运动的位移 |
9. 如图所示,某人将物体沿斜面向上拉,拉力F大小等于摩擦力,则下列说法中正确的是( )
如图所示,某人将物体沿斜面向上拉,拉力F大小等于摩擦力,则下列说法中正确的是( )
 如图所示,某人将物体沿斜面向上拉,拉力F大小等于摩擦力,则下列说法中正确的是( )
如图所示,某人将物体沿斜面向上拉,拉力F大小等于摩擦力,则下列说法中正确的是( )| A. | 物体受到的合外力为零 | |
| B. | 物体做减速运动 | |
| C. | 合外力对物体做功做负功,物体动能在减小 | |
| D. | 物体的机械能保持不变 |
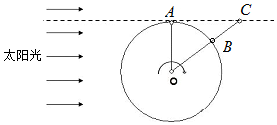 站在地球赤道某地的人,日落后4小时的时候,在自己头顶正上方观察到一颗恰好有阳光照亮的人造地球卫星,已知地球的半径为R,地球表面的重力加速度为g,太阳光可认为是平行光.若该卫星在赤道所在平面内做匀速圆周运动,求:
站在地球赤道某地的人,日落后4小时的时候,在自己头顶正上方观察到一颗恰好有阳光照亮的人造地球卫星,已知地球的半径为R,地球表面的重力加速度为g,太阳光可认为是平行光.若该卫星在赤道所在平面内做匀速圆周运动,求: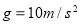 )
)