题目内容
13. a是地球赤道上一栋建筑,b是在赤道平面内做匀速圆周运动、距地面9.6×106m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图所示),请画出经30h后,a、b、c的大致位置并说明理由.(取地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,π=$\sqrt{10}$)
a是地球赤道上一栋建筑,b是在赤道平面内做匀速圆周运动、距地面9.6×106m的卫星,c是地球同步卫星,某一时刻b、c刚好位于a的正上方(如图所示),请画出经30h后,a、b、c的大致位置并说明理由.(取地球半径R=6.4×106m,地球表面重力加速度g=10m/s2,π=$\sqrt{10}$)
分析 该题主要考查同步卫星,近地卫星及赤道上的物体间的追赶问题.对于不同轨道上的追赶问题,我们要从不同卫星的角速度或周期关系出发去解决问题.
解答 解:由于a物体和同步卫星c的周期都为24h.所以30h后两物体相对于原位置转过的角度是90°,
根据万有引力提供向心力得:$G\frac{Mm}{{r}^{2}}=mr{ω}^{2}$=$m\frac{4{π}^{2}}{{T}^{2}}r$
解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$
而b的半径为9.6×106m,地球的R=6.4×106m,地球表面重力加速度g=10m/s2.
解得:Tb≈6h
30个小时转6圈,所以又回到了原位置.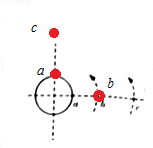
答:30h后a与c物体相对于原位置转过的角度是90°,b又回到了原位置.如图.
点评 利用题目提供的物理量找出不同卫星的角速度或周期关系,根据圆周运动知识求出转过的圈数.

练习册系列答案
相关题目
1. 在长绳的一端系一个质量为2kg的小球,绳的长度为1.6m,用绳拉着小球在竖直面内做圆周运动,若小球能通过最高点,则( )
在长绳的一端系一个质量为2kg的小球,绳的长度为1.6m,用绳拉着小球在竖直面内做圆周运动,若小球能通过最高点,则( )
 在长绳的一端系一个质量为2kg的小球,绳的长度为1.6m,用绳拉着小球在竖直面内做圆周运动,若小球能通过最高点,则( )
在长绳的一端系一个质量为2kg的小球,绳的长度为1.6m,用绳拉着小球在竖直面内做圆周运动,若小球能通过最高点,则( )| A. | 在最高点处,绳对小球一定有向下的拉力 | |
| B. | 在最低点处,绳对小球的拉力一定向上 | |
| C. | 绳最容易断的地方应该在最低点 | |
| D. | 小球通过最高点的速度不得小于4m/s |
8. 一个小球沿斜面向下运动,用每隔$\frac{1}{10}$s曝光一次的频闪相机拍摄不同时刻小球位置的照片,如图所示.即照片上出现的相邻两个小球的像之间的时间间隔为$\frac{1}{10}$s,测得小球在几个连续相等时间内位移数据见表:
一个小球沿斜面向下运动,用每隔$\frac{1}{10}$s曝光一次的频闪相机拍摄不同时刻小球位置的照片,如图所示.即照片上出现的相邻两个小球的像之间的时间间隔为$\frac{1}{10}$s,测得小球在几个连续相等时间内位移数据见表:
根据以上数据,甲、乙两同学计算小球加速度的方法如下:
甲同学:a1=$\frac{{x}_{2}-{x}_{1}}{{T}^{2}}$,a2=$\frac{{x}_{3}-{x}_{2}}{{T}^{2}}$,a3=$\frac{{x}_{4}-{x}_{3}}{{T}^{2}}$,$\overline{a}$=$\frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}$.
乙同学:a1=$\frac{{x}_{3}-{x}_{1}}{2{T}^{2}}$,a2=$\frac{{x}_{4}-{x}_{2}}{2{T}^{2}}$,$\overline{a}$=$\frac{{a}_{1}+{a}_{2}}{2}$.
你认为甲、乙两位同学中计算方法更准确的是乙,加速度值为1.10m/s2.(结果保留3位有效数字)
 一个小球沿斜面向下运动,用每隔$\frac{1}{10}$s曝光一次的频闪相机拍摄不同时刻小球位置的照片,如图所示.即照片上出现的相邻两个小球的像之间的时间间隔为$\frac{1}{10}$s,测得小球在几个连续相等时间内位移数据见表:
一个小球沿斜面向下运动,用每隔$\frac{1}{10}$s曝光一次的频闪相机拍摄不同时刻小球位置的照片,如图所示.即照片上出现的相邻两个小球的像之间的时间间隔为$\frac{1}{10}$s,测得小球在几个连续相等时间内位移数据见表:| x1/cm | x2/cm | x3/cm | x4/cm |
| 8.20 | 9.32 | 10.40 | 11.52 |
甲同学:a1=$\frac{{x}_{2}-{x}_{1}}{{T}^{2}}$,a2=$\frac{{x}_{3}-{x}_{2}}{{T}^{2}}$,a3=$\frac{{x}_{4}-{x}_{3}}{{T}^{2}}$,$\overline{a}$=$\frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}$.
乙同学:a1=$\frac{{x}_{3}-{x}_{1}}{2{T}^{2}}$,a2=$\frac{{x}_{4}-{x}_{2}}{2{T}^{2}}$,$\overline{a}$=$\frac{{a}_{1}+{a}_{2}}{2}$.
你认为甲、乙两位同学中计算方法更准确的是乙,加速度值为1.10m/s2.(结果保留3位有效数字)
18. 如图所示,A、B、C三个物块重力均为100N,小球P的重力为20N,作用在物块B上的水平向左的拉力F=30N,整个系统静止,与物块C相连的轻绳恰好水平,下列说法正确的是( )
如图所示,A、B、C三个物块重力均为100N,小球P的重力为20N,作用在物块B上的水平向左的拉力F=30N,整个系统静止,与物块C相连的轻绳恰好水平,下列说法正确的是( )
 如图所示,A、B、C三个物块重力均为100N,小球P的重力为20N,作用在物块B上的水平向左的拉力F=30N,整个系统静止,与物块C相连的轻绳恰好水平,下列说法正确的是( )
如图所示,A、B、C三个物块重力均为100N,小球P的重力为20N,作用在物块B上的水平向左的拉力F=30N,整个系统静止,与物块C相连的轻绳恰好水平,下列说法正确的是( )| A. | A和B之间的摩擦力为30N | B. | B和C之间的摩擦力为30N | ||
| C. | C与桌面之间的摩擦力为10N | D. | 物块C受到5个力的作用 |
3.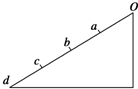 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:2:3:4 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:2:3:4 | |
| C. | 在斜面上od间运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上od间运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
 质量m=2kg的物块在倾角为θ=37°的斜面上,受一沿斜面向上的拉力F=17.2N的作用,如图从静止开始运动,已知物块与斜面间的动摩擦因数μ=0.25,sin37°=0.6,cos37°=0.8.(g取10m/s2)求:
质量m=2kg的物块在倾角为θ=37°的斜面上,受一沿斜面向上的拉力F=17.2N的作用,如图从静止开始运动,已知物块与斜面间的动摩擦因数μ=0.25,sin37°=0.6,cos37°=0.8.(g取10m/s2)求: 如图所示,物体由静止从A点沿斜面匀加速下滑,随后在水平面上作匀减速运动,最后停止于C点,已知AB=6m,BC=8m,整个运动历时12s,求物体在AB和BC运动的加速度和最大速度.
如图所示,物体由静止从A点沿斜面匀加速下滑,随后在水平面上作匀减速运动,最后停止于C点,已知AB=6m,BC=8m,整个运动历时12s,求物体在AB和BC运动的加速度和最大速度.