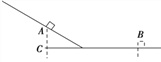
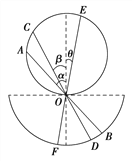
[题目]如图所示.有一半圆.其直径水平且与另一圆的底部相切于O点.O点恰好是下半圆的圆心.它们处在同一竖直平面内．现有三条光滑轨道AOB.COD.EOF.它们的两端分别位于上下两圆的圆周上.轨道与竖直直径的夹角关系为α>β>θ.现让一小物块先后从三条轨道顶端由静止下滑至底端.则小物块在每一条倾斜轨道上滑动时所经历的时间关系为( )A. tAB＝tCD 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，有一半圆，其直径水平且与另一圆的底部相切于O点，O点恰好是下半圆的圆心，它们处在同一竖直平面内．现有三条光滑轨道AOB、COD、EOF，它们的两端分别位于上下两圆的圆周上，轨道与竖直直径的夹角关系为α>β>θ，现让一小物块先后从三条轨道顶端由静止下滑至底端，则小物块在每一条倾斜轨道上滑动时所经历的时间关系为(　　)

A. tAB＝tCD＝tEF

B. tAB＞tCD＞tEF

C. tAB＜tCD＜tEF

D. tAB＝tCD＜tEF

【答案】B

【解析】试题分析：设上面圆的半径为，下面圆的半径为，则轨道的长度，下滑的加速度，根据位移时间公式得，，则，因为，则，故B正确，A、C、D错误。

考点：牛顿第二定律；匀变速直线运动的位移与时间的关系

【名师点睛】根据几何关系求出轨道的长度，结合牛顿第二定律求出物块下滑的加速度，根据位移时间公式求出物块在滑动时经历的时间大小关系。

【题型】单选题
【结束】
134

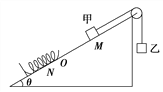
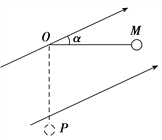
【题目】在竖直平面内有一方向斜向上且与水平方向成α＝30°角的匀强电场，电场中有一质量为m，电荷量为q的带电小球，用长为L的不可伸长的绝缘细线悬挂于O点，如图所示．开始时小球静止在M点，细线恰好水平．现用外力将小球拉到最低点P，然后由静止释放，则以下判断正确的是(　　)

A. 小球再次到M点时，速度刚好为零

B. 小球从P到M过程中，合外力对它做的功为

C. 小球从P到M过程中，其机械能增加了

D. 如果小球运动到M点时，细线突然断裂，小球将做匀变速直线运动

【答案】B

【解析】根据题述，开始时小球静止于M点，细线恰好水平，由平衡条件可知，.小球再次到M点时，切向加速度为零，速度最大，选项A错误．小球从P到M过程中，重力做负功为WG=－mgL，电场力qE做正功为,合外力对它做的功为，选项B正确．由功能关系可知，电场力做功机械能增加，小球从P到M过程中，其机械能增加了，选项C错误．由于在M点，小球所受电场力在竖直方向的分量等于重力，如果小球运动到M点时，细线突然断裂，小球将做匀变速曲线运动，选项D错误．

练习册系列答案

（1）同学们用游标卡尺测量玻璃管的内径d；向玻璃管内注满自来水，并用刻度尺测量水柱长度L；用多用电表的电阻“×100”档，按正确的操作步骤测量此水柱体的电阻R，表盘的示数如图所示；由图所示可知玻璃管的内径d=_______mm，水柱体的电阻R=______Ω．

（2）该小组同学想用伏安法更精确地测量其电阻R，现有的器材及其代号和规格如下：

电压表V（量程15V，内阻约30kΩ）；电流表A（量程300mA，内阻约50Ω）；滑动变阻器R0（0～100Ω，允许最大电流1A）；电池组E（电动势E=12V，内阻r=6Ω）；开关一个、导线若干．请根据情况补全电路原理图（并不是所有的接线点都要连接）________

（3）如果测出水柱的长度L、玻璃管的内径d和水柱的电阻R，则自来水电阻率的表达式为ρ=________．（用符号表示）

【题目】如图所示，在绝热圆柱形汽缸中用光滑绝热活塞密闭有一定质量的理想气体，在汽缸底部开有一小孔，与U形水银管相连，外界大气压为P0=75cmHg，缸内气体温度t0=27℃，稳定后两边水银面的高度差为△h=1.5cm，此时活塞离容器底部的高度为L=50cm（U形管内气体的体积忽略不计）．已知柱形容器横截面S=0.01m2，取75cmHg压强为1.0×105Pa，重力加速度g=10m/s2．

（i）求活塞的质量；

（ii）若容器内气体温度缓慢降至-3℃，求此时U形管两侧水银面的高度差△h′和活塞离容器底部的高度L′．

【题目】如图所示，10匝矩形线框，在磁感应强度为0.4 T的匀强磁场中，绕垂直磁场的轴OO′以角速度为100 rad/s匀速转动，线框电阻不计，面积为0.5m2，线框通过滑环与一理想变压器的原线圈相连，副线圈接有两只灯泡L1和L2.已知变压器原、副线圈的匝数比为10：1，开关断开时L1正常发光，且电流表示数为0.01A，则(　　)

A. 若从图示位置开始计时，线框中感应电动势的瞬时值为200sin100t V

B. 灯泡L1的额定功率为2W

C. 若开关S闭合，灯泡L1将更亮

D. 若开关S闭合，电流表示数将增大

【答案】D

【解析】试题分析：先根据公式Um=NBSω求解输入电压的最大值，然后根据理想变压器的变压比公式和变流比公式列式求解．

解：A、变压器的输入电压的最大值为：Um=NBSω=10×0.4×0.5×100=200V

从垂直中性面位置开始计时，故线框中感应电动势的瞬时值为：u=Umcosωt=200cos100t（V），故A错误；

B、变压器输入电压的有效值为：

U1===100V

开关断开时L1正常发光，且电流表示数为0.01A，根据变流比公式，有：

故I1=0.1A

灯泡L1的额定功率等于此时变压器的输入功率，为：

P=U1I1=100×0.1=10W，故B错误；

C、若开关S闭合，输出电压不变，故灯泡L1亮度不变；故C错误；

D、若开关S闭合，输出电压不变，输出端电阻减小，故输出电流增加，故输入电流也增加，输入功率增加，灯泡L1将更亮；故D正确；

故选：D．

点评：本题关键是记住交流发电机最大电动势表达式Um=NBSω，同时要明确输入电压决定输出电压，输出电流决定输入电流，输出功率决定输入功率．

【题型】单选题
【结束】
153

【题目】在如图所示的电路中，开关闭合后，当滑动变阻器的触头P向下滑动时，有(　　)

A. 灯L1变亮

B. 灯L2变暗

C. 电源的总功率变大

D. 电阻R1有从b到a方向的电流

【题目】如图为“验证动能定理”的实验装置．钩码质量为m，小车和砝码的总质量M＝300g．实验中用钩码重力的大小作为细绳对小车拉力的大小．实验主要过程如下：

①安装实验装置；

②分析打点计时器打出的纸带，求出小车的速度；

③计算小车的动能增量和对应细绳拉力做的功，判断两者是否相等．

(1)以下关于该实验的说法中正确的是________．

A．调整滑轮高度使细绳与木板平行

B．为消除阻力的影响，应使木板右端适当倾斜

C．在质量为10g、50g、80g的三种钩码中，挑选质量为80g的钩码挂在挂钩P上最为合理

D．先释放小车，然后接通电源，打出一条纸带

(2)在多次重复实验得到的纸带中选择点迹清晰的一条．测量如图，打点周期为T，当地重力加速度为g.用题中的有关字母写出验证动能定理的表达式________．

(3)写出两条引起实验误差的原因________________________；________________________.

【答案】 AB 长度测量的误差用mg代替绳子的拉力

【解析】解决实验问题首先要掌握该实验原理，了解实验的操作步骤和数据处理以及注意事项，了解平衡摩擦力的方法；由匀变速运动的推论求出滑块的瞬时速度，代入动能定理表达式即可正确解题。

(1)小车运动中受到重力、支持力、绳的拉力、摩擦力四个力的作用．首先若要使小车受到合力等于绳上的拉力，必须保证：摩擦力被平衡、绳的拉力平行于接触面，故A、B正确；在保证钩码重力等于细绳上的拉力及上述前提下对小车有：，对钩码：，解之有，可见只有当时才有，故应选用10g的钩码最为合理，C错误．打点计时器的使用要求是先接通电源，待其工作稳定后再释放小车，D错误．

(2)由题图知、，故动能变化量为，合力所做功，故需验证的式子为

(3)从产生的偶然误差考虑有长度测量的误差；从系统误差产生的角度考虑有用mg代替绳子的拉力、电源频率不稳定、摩擦力未完全被平衡等引起的误差(答案合理皆可)．

【题型】实验题
【结束】
90

【题目】某探究小组要尽可能精确地测量电流表○A1 的满偏电流，可供选用的器材如下：

A.待测电流表A1 (满偏电流Imax约为800 μA、内阻r1约为100Ω，表盘刻度均匀、总格数为N)

B.电流表A2 (量程为0.6 A、内阻r2＝0.1Ω)

C.电压表V (量程为3V、内阻RV＝3kΩ)

D.滑动变阻器R(最大阻值为20 Ω)

E.电源E(电动势有3V、内阻r约为1.5Ω)

F.开关S一个，导线若干

(1)该小组设计了图甲、图乙两个电路图，其中合理的是________(选填“图甲”或“图乙”)．

(2)所选合理电路中虚线圈处应接入电表________(选填“B”或“C”)．

(3)在开关S闭合前，应把滑动变阻器的滑片P置于________端(选填“a”或“b”)．

(4)在实验中，若所选电表的读数为Z，电流表A1的指针偏转了n格，则可算出待测电流表A1的满偏电流Imax＝________.

【题目】倾角θ＝30°的斜面体固定在水平面上，在斜面体的底端附近固定一挡板，一质量不计的弹簧下端固定在挡板上，弹簧自然伸长时其上端位于斜面体上的O点处．质量分别为4m、m的物块甲和乙用一质量不计的细绳连接，跨过固定在斜面体顶端的光滑定滑轮，如图所示．开始物块甲位于斜面体上的M处，且MO＝L，物块乙开始距离水平面足够远，现将物块甲和乙由静止释放，物块甲沿斜面下滑，当物块甲将弹簧压缩到N点时，物块甲、乙的速度减为零，ON＝.已知物块甲与斜面体之间的动摩擦因数为μ＝，重力加速度取g＝10 m/s2，忽略空气的阻力，整个过程细绳始终没有松弛．则下列说法正确的是(　　)

A. 物块甲由静止释放到斜面体上N点的过程，物块甲先做匀加速直线运动，紧接着做匀减速直线运动直到速度减为零

B. 物块甲在与弹簧接触前的加速度大小为0.5 m/s2

C. 物块甲位于N点时，弹簧所储存的弹性势能的最大值为mgL

D. 物块甲位于N点时，弹簧所储存的弹性势能的最大值为mgL

【答案】BC

【解析】释放物块甲、乙后，物块甲沿斜面加速下滑，当与弹簧接触时，开始压缩弹簧，弹簧产生沿斜面向上的弹力，物块甲做加速度减小的加速运动，当把弹簧压缩到某一位置时，物块甲沿斜面受力平衡，速度达到最大，之后物块甲做加速度增大的减速运动，A错误；对物块甲、乙，根据牛顿第二定律有，其中，解得，B正确；以物块甲和乙为研究对象，从M点运动到N点，在N点弹簧压缩最短，弹性势能最大，由动能定理得，解得，弹性势能的变化量，C正确，D错误。