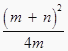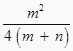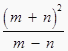题目内容
【题目】把水星和金星绕太阳的运动视为匀速圆周运动。从水星与金星和太阳在一条直线上开始计时，若测得在相同时间内水星，金星转过的角度分别为
、
（均为锐角），则由此条件可求得水星和金星
A. 质量之比
B. 绕太阳运动的轨道半径之比
C. 绕太阳运动的动能之比
D. 受到太阳的引力之比
【答案】B
【解析】试题分析：相同时间内水星转过的角度为
；金星转过的角度为
，可知道它们的角速度之比，绕同一中心天体做圆周运动，根据万有引力提供向心力，可求出轨道半径比，由于不知道水星和金星的质量关系，故不能计算它们绕太阳的动能之比，也不能计算它们受到的太阳引力之比．
水星和金星作为环绕体，由题可求出周期或角速度之比，但无法它们求出质量之比，A错误；相同时间内水星转过的角度为θ1；金星转过的角度为θ2，可知道它们的角速度之比，根据万有引力提供向心力
，解得
，知道了角速度比，就可求出轨道半径之比，即到太阳的距离之比，B正确；由于不知道水星和金星的质量关系，故不能计算它们绕太阳的动能之比，C错误；由于不知道水星和金星的质量关系，故不能计算它们受到的太阳引力之比，D错误．
练习册系列答案
相关题目
