题目内容
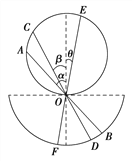
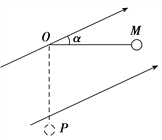
【题目】如图所示,xoy坐标系建在光滑绝缘的水平面上,x轴下方存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直水平面向外。A、C、D坐标分别为(0,2L)、(0,L)、 (a,0),A、C两点分别固定一平行于x轴放置的长度小于a的相同绝缘弹性挡板PQ和MN,A、C均为挡板中点,A、D两处分别放有两个相同的绝缘小球(可视为质点),小球质量为m,且A处小球不带电,D处小球带电量为q(q>0).若A处小球以某一水平速度v0飞向D,带电小球被碰后与挡板MN发生两次碰撞,并能经过A点与档板PQ发生碰撞,设球与球发生弹性碰撞,球与挡板碰撞前后沿板方向分速度不变,垂直板方向分速度等大反向,求:
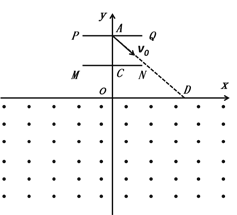
(l)A处小球的初速度v0的大小?
(2)弹性档板MN的最小长度?
(3)若a= ![]() ,则带电小球运动的时间?
,则带电小球运动的时间?
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】(1)两小球策一次弹性碰撞![]() ,
,![]()
解得![]()
带电小球在磁场中运动半径![]() ,
,![]() ,得
,得![]()
在粒子没射向A点前,每次进入磁场与下次射出磁场两点间距![]()
由几何知识可知,粒子每次射出磁场与下次进入磁场两点间距![]()
带电小球两次碰撞到达A点,由对称性可知:![]()
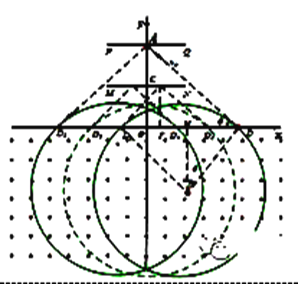
由以上各式可得:![]()
(2)由几何知识可知,![]()
由图可知板的最短长度为![]() ,得
,得![]() (或由图可知
(或由图可知![]() )
)
(3)若![]() ,则
,则![]() ,带电小球在磁场中运动的圆心角为
,带电小球在磁场中运动的圆心角为![]() ,
,
做匀速直线运动的中路程![]() ,
,![]()
带电小球在D处第二次与不带电小球碰撞,同理可知两次交换速度,带电小球停在D处,不带电小球匀速直线运动。所以,带电小球的运动时间![]()
由以上得![]() ;
;

练习册系列答案
相关题目