题目内容
16.质量为1kg的重锤自由下落,通过打点计时器在纸带上记录运动过程,打点计时器所接电源为6V、50Hz的交流电源.如图1所示,纸带上O点为重锤自由下落时纸带打点起点,选取的计数点A、B、C、D、E、F、G依次间隔一个点(图中未画出),各计数点与O点距离依次为31.4mm、70.6mm、125.4mm、195.9mm、282.1mm、383.8mm、501.2mm,重力加速度取9.8m/s2.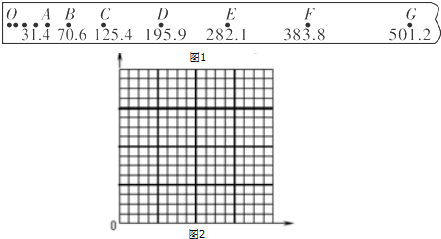
(1)求出B、C、D各点速度并填入下表.
| 计数点 | B | D | F |
| 速度/(m•s-1) |
| 计数点 | B | D | F |
| 功(J) |
分析 纸带实验中,若纸带匀变速直线运动,根据时间中点的瞬时速度等于该过程中的平均速度可计算出打出某点时纸带运动的瞬时速度.
根据功的定义式,计算重力做功的数值.
作出W-v2图象,找出重力做功与速度的相关量之间的关系.
解答 解:(1)各点速度由公式v=$\overline{v}$=$\frac{△x}{△t}$
求出:
vB=$\overline{v}$AC=$\frac{{x}_{AC}}{2T}$=$\frac{125.4-31.4}{4×0.02}×1{0}^{-3}$ m/s=1.18m/s
同理:vC=1.57m/s,vD=1.96m/s,vE=2.35m/s,vF=2.74m/s
(2)重力的功由W=mg△x求出:WB=mg$\overline{OB}$=1×9.80×70.6×10-3J=0.692J
同理WC=1.23J,WD=1.92J,WE=2.76J,WF=3.76J
(3)图象如上图所示,图中纵坐标表示重力的功WG,横坐标表示速度的二次方v2,由图线可见,重力的功WG与速度的二次方v2成正比.
故答案为:(1)1.18;1.57;1.96;2.35;2.74;
(2)0.692;1.23;1.92;2.76;3.76;
(3)重力的功WG;速度的二次方v2.
点评 本题探究重力做功与速度变化之间的关系,通过对打点计时器在纸带上打出的点的分析,我们可以由公式v=$\overline{v}$=$\frac{△x}{△t}$ 求出各点的速度,重力的功由W=mg△x求出.我们无法直接由一些数据得出规律性的结论,故借助于图象分析法,而最容易想到的是W与v的关系,但得到的图线无法下结论,故W-v2图线,进而得出结论.

练习册系列答案
相关题目
18.已知直线AC的中点为B点,物体沿AC做变速直线运动,在AB段的平均速度为6m/s,在BC段的平均速度为4m/s,那么它在AC段的平均速度是( )
| A. | 4.8 m/s | B. | 5.0 m/s | C. | 5.2 m/s | D. | $\sqrt{13}$ m/s |
7.下列说法的正确的是( )
| A. | “油膜法“估测分子大小实验中,可将纯油酸直接滴入浅盘的水面上 | |
| B. | 彩色液晶显示器利用了液晶的光学性质具有各向异性的特点 | |
| C. | 气体被压缩时有时需要用较大的力,这是因为气体被压缩时其分子间的分子力表现为斥力 | |
| D. | 外界对物体做功,物体的内能可能减小 |
11.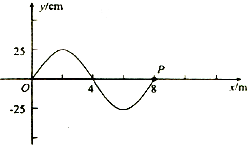 一简谐横波从O点沿x轴正方向传播,在t=0时刻的波形图如图甲所示,此时该波刚传到x=8m处.再经过1.4s时,P质点第2次出现波峰,则( )
一简谐横波从O点沿x轴正方向传播,在t=0时刻的波形图如图甲所示,此时该波刚传到x=8m处.再经过1.4s时,P质点第2次出现波峰,则( )
 一简谐横波从O点沿x轴正方向传播,在t=0时刻的波形图如图甲所示,此时该波刚传到x=8m处.再经过1.4s时,P质点第2次出现波峰,则( )
一简谐横波从O点沿x轴正方向传播,在t=0时刻的波形图如图甲所示,此时该波刚传到x=8m处.再经过1.4s时,P质点第2次出现波峰,则( )| A. | 在x=10m处的接收装置,接收到机械波的频率为1.25Hz | |
| B. | 该波遇到障碍发生明显衍射现象,障碍物尺寸必为8m | |
| C. | 再经过△t=1.4s,坐标为x=16m处的质点第一次出现波峰 | |
| D. | 再经过△t=1s,P点处于波峰 | |
| E. | P点的振动方程为y=25sin2.5πt(cm) |
1.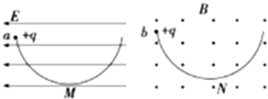 如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )
如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )
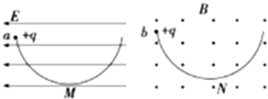 如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )
如图所示,两个相同的半圆形光滑绝缘轨道分别竖直放置在匀强电场E和匀强磁场B中,轨道两端在同 一高度上,两个相同的带正电小球a、b同时从轨道左端最高点由静止释放,且在运动过程中始终能通过各自轨道的最低点M、N,则( )| A. | 两小球某次到达轨道最低点时的速度不可能有υN=υM | |
| B. | 两小球都能到达轨道的最右端 | |
| C. | 小球b第一次到达N点的时刻与小球a第一次到达M点的时刻相同 | |
| D. | 小球a受到的电场力一定不大于a的重力,小球b受到的最大洛伦兹力可能大于b的重力 |
5.物体静止于倾角为θ的斜面上,当斜面倾角θ变小时,物体所受力的变化情况是( ) 

| A. | 重力、支持力、静摩擦力均增大 | |
| B. | 重力不变,支持力增大,静摩擦力减小 | |
| C. | 重力不变,支持力、静摩擦力增大 | |
| D. | 以上说法都不对 |
 用多用电表的欧姆挡测量一未知电阻的阻值.若将选择倍率的旋钮拨至“×100Ω”挡,测量时指针停在刻度盘0Ω附近处,为了提高测量的精确性,有下列可供选择的步骤:
用多用电表的欧姆挡测量一未知电阻的阻值.若将选择倍率的旋钮拨至“×100Ω”挡,测量时指针停在刻度盘0Ω附近处,为了提高测量的精确性,有下列可供选择的步骤: