题目内容
8.某人骑自行车以4m/s的速度匀速前进,某时刻在他前面7m 处以10m/s的速度同向行驶的汽车开始关闭发动机,而以2m/s2的加速度减速前进.求:(1)自行车和汽车何时相距最远?
(2)自行车和汽车最远距离为多少?
(3)此人需要多长时间才能追上汽车?
分析 在自行车追赶汽车的过程中,当两车的速度相等时,两车的距离最大.在自行车追上汽车时,它们的位移之差等于24m,由此可以求得需要的时间
解答 解:(1)当两者速度相同时,两者相距最远,由速度公式得:
Vt=V0+at
t=$\frac{{v}_{t}-{v}_{0}}{a}=\frac{10-4}{2}s$=3s
(2)两者速度相同时,汽车的位移为:
X汽=V汽t+$\frac{1}{2}$a汽t2=$10×3-\frac{1}{2}2×{3}^{2}m$=21m
自行车的位移为:
X自=V自t=4×3m=12m
两者相距距离为:
X,=X汽+d-X自=21+7-12m=16m
(3)汽车减速运动到静止所需时间为t,则
由v=at得:
t=$\frac{v}{a}$=$\frac{10}{2}s$=5 s
在这段时间内,自行车的位移
X1=v1t=4×5m=20 m
汽车的位移
X2=$\frac{v}{2}$t=$\frac{10}{2}×5m$=25 m
可见,当汽车停止运动时,人并未追上汽车,此时人和汽车之间的距离
X=d+X2-X1=7+25-20m=12 m
人追上汽车所需的时间
t总=t+$\frac{x}{{v}_{自}}$=$5+\frac{12}{4}s$=8 s
答:(1)自行车和汽车3s时相距最远?
(2)自行车和汽车最远距离为16m
(3)此人需要8s才能追上汽车?
点评 汽车的追及相遇问题,一定要掌握住汽车何时相遇、何时距离最大这两个问题,这道题是典型的追及问题,同学们一定要掌握住

 如图所示,为沿x轴正方向传播的一列简谐横波在某时刻的波形图,其波速为200m/s,则下列说法正确的是( )
如图所示,为沿x轴正方向传播的一列简谐横波在某时刻的波形图,其波速为200m/s,则下列说法正确的是( )| A. | 从图示时刻开始,经0.01s质点a通过的路程为40cm,此时相对平衡位置的位移为零 | |
| B. | 图中质点b的加速度在增大 | |
| C. | 从图示时刻开始,经0.01s质点b位于平衡位置上方,并向上做减速运动 | |
| D. | 若要产生明显的衍射现象,该波所遇到障碍物的尺寸一定小于4m |
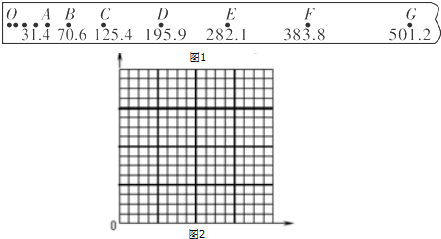
(1)求出B、C、D各点速度并填入下表.
| 计数点 | B | D | F |
| 速度/(m•s-1) |
| 计数点 | B | D | F |
| 功(J) |
| A. | 车从出发到B杆所用时间为9 s | B. | 车的加速度为15 m/s2 | ||
| C. | 经过A杆时速度为5 m/s | D. | 从出发点到A杆的距离为7.5 m |
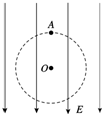 如图所示,在方向竖直向下的匀强电场中,一个带负电的小球被绝缘细绳拴着在竖直平 面内做圆周运动.则( )
如图所示,在方向竖直向下的匀强电场中,一个带负电的小球被绝缘细绳拴着在竖直平 面内做圆周运动.则( )| A. | 小球不可能做匀速圆周运动 | |
| B. | 小球运动到最高点绳子的拉力一定最小 | |
| C. | 当小球运动到最高点时电势能最小 | |
| D. | 小球在运动过程中,机械能一定不守恒 |
| A. | 用冰袋给高热病人降温,原因是冰熔化要吸热 | |
| B. | 烧开水时壶嘴冒“白气”,属于液化现象 | |
| C. | 放在衣柜里的樟脑丸过一段时间表小了,属于汽化现象 | |
| D. | 洒在教室地面上的水过一会儿变干了属于升华现象 |
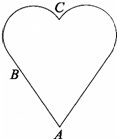
| A. | 导体表面电荷分布均匀区 | B. | A处电荷分布最疏 | ||
| C. | C处几乎没有电荷 | D. | B处电荷分布最疏 |
 小球做直线运动时的频闪照片如图所示.已知频闪周期T=0.1s,小球相邻位置的间距(由照片中的刻度尺量得)分别为OA=6.50cm,AB=5.90cm,BC=5.30cm,
小球做直线运动时的频闪照片如图所示.已知频闪周期T=0.1s,小球相邻位置的间距(由照片中的刻度尺量得)分别为OA=6.50cm,AB=5.90cm,BC=5.30cm,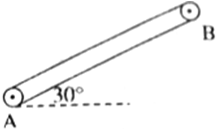 如图所示,10m长的传送带动摩擦因数为$\frac{\sqrt{3}}{2}$,倾角为30o,用电动机带动,其运行速度大小为2m/s,运行方向为顺时针,现将质量为40kg的麻包轻放在传送带的下端.(重力加速度取10m/s2)试求:
如图所示,10m长的传送带动摩擦因数为$\frac{\sqrt{3}}{2}$,倾角为30o,用电动机带动,其运行速度大小为2m/s,运行方向为顺时针,现将质量为40kg的麻包轻放在传送带的下端.(重力加速度取10m/s2)试求: