题目内容
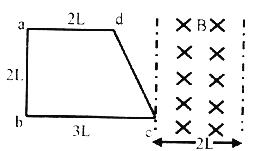
【题目】如图所示，质量为M的长木板静止在光滑水平面上，上表面OA段光滑，AB段粗糙且长为l，左端O处固定轻质弹簧，右侧用不可伸长的轻绳连接于竖直墙上，，轻绳所能承受的最大拉力为F．质量为m的小滑块以速度v从A点向左滑动压缩弹簧，弹簧的压缩量达最大时细绳恰好被拉断，再过一段时间后长木板停止运动，小滑块恰未掉落。则（ ）
A. 细绳被拉断瞬间木板的加速度大小为
B. 细绳被拉断瞬间弹簧的弹性势能为
C. 弹簧恢复原长时滑块的动能为
D. 滑块与木板AB间的动摩擦因数为
【答案】ABD
【解析】试题分析：细绳恰好被拉断时，弹簧的弹力等于F，由木板，利用牛顿第二定律求加速度。根据机械能守恒定律求细绳被拉断瞬间弹簧的弹性势能。细绳被拉断后，滑块与木板组成的系统动量守恒，由动量守恒定律和能量守恒定律结合求动摩擦因数．
细绳被拉断瞬间，对木板分析，由于OA段光滑，没有摩擦力，在水平方向上只受到弹簧给的弹力，细绳被拉断瞬间弹簧的弹力等于F，故
，解得
，A错误；细绳被拉断瞬间弹簧的压缩量达最大，弹性势能最大，B错误；弹簧恢复原长时木板获得的动能，所以滑块的动能小于
，C错误；由于细绳被拉断瞬间，木板速度为零，小滑块速度为零，所以小滑块的动能全部转化为弹簧的弹性势能，即
，小滑块恰未掉落时滑到木板的右端，且速度与木板相同，设为
，取向左为正方向，由动量守恒定律和能量守恒定律得
，
，联立解得
，D正确．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
