题目内容
【题目】如图所示,倾角为θ、半径为R的倾斜圆盘绕圆心处的转轴O以角速度ω匀速转动,一个质量为m的小物块放在圆盘的边缘,小物块与圆盘间的动摩擦因数为μ。图中A、B分别为小物块转动过程中所经过的最高点和最低点,运动过程中经过的C、D两点连线与AB垂直,小物块与圆盘间的最大静摩擦力等于滑动摩擦力,且始终相对于圆盘静止。重力加速度为g,下列说法正确的是 ( )
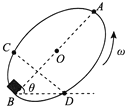
A. 小物块受到的摩擦力始终指向圆心
B. 动摩擦因数μ一定大于tanθ
C. 小物块从A点运动到B点的过程中,摩擦力对小物块做功为-μmgπRcosθ
D. 当小物块运动至C、D两点时所受摩擦力大小相等,从C点运动到D点的过程中摩擦力对小物块先做负功后做正功
【答案】BD
【解析】小物块所受重力沿圆盘的分力及静摩擦力的合力提供向心力,始终指向圆心,选项A错误;小物块在B点时由牛顿第二定律Ff-mgsinθ=mRω2,Ff>mgsinθ,又因为Ff<μmgcosθ,所以μmgcosθ>mgsinθ,则μ一定大于tanθ,选项B正确;小物块从A点运动到B点的过程中由动能定理:mg2Rsinθ+WFf=0解得WFf =-mg2Rsinθ,选项C错误;小物块运动到CD两点时受力具有对称性的特点,所受的静摩擦力大小相等,方向关于AB对称,从C点运动到D点的过程中,重力先做正功后做负功,小物块动能始终不变,即合外力做功始终为零,所以摩擦力对小物块先做负功后做正功,选项D正确;故选BD.

练习册系列答案
相关题目