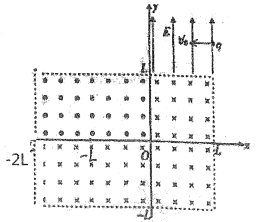
[题目]如图所示.水平光滑细杆上P点套一小环.小环通过长L=1m的轻绳悬挂一夹子.夹子内夹有质量m=1kg的物块.物块两竖直侧面与夹子间的最大静摩擦力均为fm=7N．现对物块施加F=8N的水平恒力作用.物块和小环一起沿水平方向做初速度为零的匀加速直线运动.小环碰到杆上的钉子Q时立即停止运动.物块恰好相对夹子滑动.此时夹子立即锁定物块.锁定题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，水平光滑细杆上P点套一小环，小环通过长L=1m的轻绳悬挂一夹子，夹子内夹有质量m=1kg的物块，物块两竖直侧面与夹子间的最大静摩擦力均为fm=7N．现对物块施加F=8N的水平恒力作用，物块和小环一起沿水平方向做初速度为零的匀加速直线运动，小环碰到杆上的钉子Q时立即停止运动，物块恰好相对夹子滑动，此时夹子立即锁定物块，锁定后物块仍受恒力F的作用。小环和夹子的大小及质量均不计，物块可看成质点，重力加速度g=10m/s2．求：

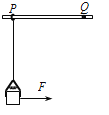
（1）物块做匀加速运动的加速度大小a；

（2）P、Q两点间的距离s；

（3）物块向右摆动的最大高度h。

【答案】（1）a=8ms/2（2）s=0.25m（3）h=1m

【解析】(1)由牛顿第二定律F=ma

解得a=4ms/2

(2)环到达Q，刚达到最大静摩擦力

由牛顿第二定律

解得vm=2m/s

根据动能定理

解得s=0.25m

(3)设物块上升的最大高度为h，水平距离为x，

由动能定理得

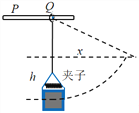
由几何关系得或

解得h =1m 或m（舍去）

练习册系列答案

相关题目

【题目】如图所示，在直角坐标系x0y平面的一、四个象限内各有一个边长为L的正方向区域，二三像限区域内各有一个高L，宽2L的匀强磁场，其中在第二象限内有垂直坐标平面向外的匀强磁场，第一、三、四象限内有垂直坐标平面向内的匀强磁场，各磁场的磁感应强度大小均相等，第一象限的x<L，L<y<2L的区域内，有沿y轴正方向的匀强电场。现有一质量为四电荷量为q的带负电粒子从坐标(L，3L/2)处以初速度沿x轴负方向射入电场，射出电场时通过坐标(0，L)点，不计粒子重力。

(1)求电场强度大小E；

(2)为使粒子进入磁场后途经坐标原点0到达坐标(-L，0)点，求匀强磁场的磁感应强度大小B；

(3)求第(2)问中粒子从进入磁场到坐标(-L，0)点所用的时间。

【题目】如图所示，在竖直平面(纸面)固定一内径很小内壁光滑的圆管形轨道ABC，它由两个半径均为R的四分之一圆管顺接而成，A与C端切线水平。在足够长的光滑水平台面上静置一个光滑圆弧轨道DE，圆弧轨道D端上缘恰好与圆管轨道的C端内径下缘水平对接。一质量为m的小球(可视为质点)以某一水平速度从A点射入圆管轨道，通过C点后进入圆弧轨道运动，过C点时轨道对小球的压力为2mg,小球始终没有离开圆弧轨道。已知圆弧轨道DE的质量为2m,重力加速度为g。求：

(1)小球从A点进入圆管轨道的速度大小；

(2)小球沿圆弧轨道上升的最大高度。

【题目】如图所示，一定量的理想气体最初处于状态A，之后经历从状态A→状态B→状态C的系列变化。已知状态A时气体的温度为200K，体积为40L，压强为8×104Pa，状态B时温度升高至400K。

①求状态B时的压强及状态C时的体积。

②从状态B到状态C的过程，定性分析气体与外界热传递的情况并求外界对气体做功的大小。

【题目】如图所示，质量为M的长木板静止在光滑水平面上，上表面OA段光滑，AB段粗糙且长为l，左端O处固定轻质弹簧，右侧用不可伸长的轻绳连接于竖直墙上，，轻绳所能承受的最大拉力为F．质量为m的小滑块以速度v从A点向左滑动压缩弹簧，弹簧的压缩量达最大时细绳恰好被拉断，再过一段时间后长木板停止运动，小滑块恰未掉落。则（　　）

A. 细绳被拉断瞬间木板的加速度大小为

B. 细绳被拉断瞬间弹簧的弹性势能为

C. 弹簧恢复原长时滑块的动能为

D. 滑块与木板AB间的动摩擦因数为

【题目】如图所示，一个可视为质点的物块，质量为m=lkg，从光滑四分之一圆弧轨道顶端由静止滑下，到达底端时恰好进入与圆弧轨道底端相切的水平传送带，传送带由电动机驱动着匀速逆时针转动，速度大小为v=3m/s.已知圆弧轨道半径R=0.45m，物块与传送带间的动摩擦因数为μ=0.1，两皮带轮之间的距离为L=4m，物块滑到圆弧轨道底端时对轨道的作用力为F，物块与传送带摩擦产生的热量为Q.重力加速度取g=10m/s2.下列说法正确的是

A. F=10N B. F=20N C. Q=10J D. Q=4J

【题目】如图所示的直角坐标系中，在直线x=－8L到y轴区域内存在着两个大小相等、方向相反的有界匀强电场，其中x轴上方的电场方向沿、轴负方向，x轴下方的电场方向沿y轴正方向。在x>0的区域内存在着垂直纸面的匀强磁场(图中未画出)，磁感应强度的大小B=。在电场左边界坐标为(一8L，－4L)的A点和坐标为(－8L，－L)的C点，将质量为m、电荷量为q的带正电粒子，先后以相同的速度v0沿x轴正方向射入电场.从A点射入的粒子，恰好从y轴上坐标为(0，4L)的A′点以速度v0沿ⅹ轴正方向射出电场，其运动轨迹如图所示。不计粒子的重力及它们之间的相互作用。