题目内容
5. 如图所示,矩形线圈的匝数为n,面积为S,电阻为r,线圈在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω匀速转动,外电路电阻为R,在线圈由图示位置转过90°的过程中,求:
如图所示,矩形线圈的匝数为n,面积为S,电阻为r,线圈在磁感应强度为B的匀强磁场中绕OO′轴以角速度ω匀速转动,外电路电阻为R,在线圈由图示位置转过90°的过程中,求:(1)通过电阻R的电荷量q;
(2)电压表的读数
(3)电阻R上产生的焦耳热Q.
分析 由法拉第电磁感应定律可求得平均电动势,再由欧姆定律求出平均电流,由Q=It可求出电荷量
求出交流电的最大值,再由有效值与最大值的关系即可求出电压的有效值;
由焦耳定律求出热量.
解答 解:(1)在此过程中,穿过线圈的磁通量变化量
△Φ=BS
经历时间△t=$\frac{1}{4}$×$\frac{2π}{ω}$=$\frac{π}{2ω}$
由平均电动势公式 E=n$\frac{△Φ}{△t}$
由欧姆定律得I=$\frac{E}{R+r}$
电荷量 q=I△t可得
通过R的电荷量q=n$\frac{△Φ}{R+r}$=$\frac{nBS}{R+r}$.
(2)产生的感应电动势的最大值为Em=nBSω
电动势的有效值为E=$\frac{Em}{\sqrt{2}}$=$\frac{nBSω}{\sqrt{2}}$
由闭合电路欧姆定律得,回路中电流的有效值为
I=$\frac{E}{R+r}$=$\frac{nBsω}{\sqrt{2}(R+r)}$
电压表的读数即为R两端的电压
U=IR=$\frac{nBsω}{\sqrt{2}(R+r)}$×R=$\frac{nBsωR}{\sqrt{2}(R+r)}$
(3)该过程中电阻R上产生的热量为
Q=I2R△t=($\frac{nBsω}{\sqrt{2}(R+r)}$)2R×$\frac{π}{2ω}$=$\frac{πωR(nBs)^{2}}{4(R+r)^{2}}$.
答:(1)通过电阻R的电荷量$\frac{nBS}{R+r}$
(2)电压表的读数$\frac{nBsωR}{\sqrt{2}(R+r)}$
(3)电阻R上产生的焦耳热$\frac{πωR{(nBs)}^{2}}{4{(R+r)}^{2}}$
点评 本题考查有效值及平均值,在解题时要注意,当求电功、电压表示数时一律用有效值;而求电量时要用平均值

 全优点练单元计划系列答案
全优点练单元计划系列答案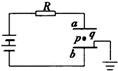 如图所示,平行板a、b组成的电容器与电池E连接,平行板电容器P处固定放置一带负电的点电荷,平行板b接地,现将电容器的b板向下稍微移动,则( )
如图所示,平行板a、b组成的电容器与电池E连接,平行板电容器P处固定放置一带负电的点电荷,平行板b接地,现将电容器的b板向下稍微移动,则( )| A. | 点电荷所受电场力增大 | B. | 点电荷在P处的电势能减少 | ||
| C. | P点电势减小 | D. | 电容器的带电量增加 |
| A. | 物体吸收热量,内能一定增大 | |
| B. | 物体放出热量,同时对外做功,内能一定减少 | |
| C. | 物体体积改变,内能可能不变 | |
| D. | 不可能从单一热源吸收热量,使之完全变为功 | |
| E. | 0℃水的内能比0℃冰的内能大 |
 如图所示,甲物体在水平力F作用下静止在乙物体上,乙物体静止在水平地面上.现增大外力F,两物体仍然静止,则下列说法中正确的是( )
如图所示,甲物体在水平力F作用下静止在乙物体上,乙物体静止在水平地面上.现增大外力F,两物体仍然静止,则下列说法中正确的是( )| A. | 乙物体对水平地面的摩擦力一定增大 | |
| B. | 乙物体对水平地面的压力一定增大 | |
| C. | 甲物体对乙物体的摩擦力一定增大 | |
| D. | 甲物体对乙物体的摩擦力一定沿斜面向上 |
 某车辆缓冲装置的理想模型如图,劲度系数足够大且为k的轻质弹簧与轻杆相连,轻杆可沿固定在车上的槽内移动,与槽间的滑动摩擦力恒为f.轻杆沿槽向左移动不超过l时,装置可安全工作.小车总质量为m.若小车以速度v0撞击固定在地面的障碍物,将导致轻杆沿槽向左移动$\frac{l}{2}$.已知轻杆与槽间的最大静摩擦力等于滑动摩擦力,不计小车与地面的摩擦.则( )
某车辆缓冲装置的理想模型如图,劲度系数足够大且为k的轻质弹簧与轻杆相连,轻杆可沿固定在车上的槽内移动,与槽间的滑动摩擦力恒为f.轻杆沿槽向左移动不超过l时,装置可安全工作.小车总质量为m.若小车以速度v0撞击固定在地面的障碍物,将导致轻杆沿槽向左移动$\frac{l}{2}$.已知轻杆与槽间的最大静摩擦力等于滑动摩擦力,不计小车与地面的摩擦.则( )| A. | 轻杆开始移动时,弹簧的压缩量为$\frac{f}{k}$ | |
| B. | 小车速度为0时,弹簧的弹性势能为$\frac{1}{2}$mv02 | |
| C. | 小车被弹回时速度等于$\sqrt{{v}_{0}^{2}-\frac{fl}{2m}}$ | |
| D. | 为使装置安全工作,允许该小车撞击的最大速度等于$\sqrt{{v}_{0}^{2}+\frac{fl}{m}}$ |

| A. | 1、2两点的场强相等 | B. | 1、2两点的电势相等 | ||
| C. | 2、3两点的场强相等 | D. | 2、3两点的电势相等 |

 如图,半径为R(O点为圆心,OC=R)光滑$\frac{1}{4}$圆轨道竖直放置,最高点C的切线水平,一个质量均为m的小球A沿圆轨道外侧运动,通过最高点时对轨道压力为0.75mg,另一个质量为2m 的B球沿圆轨道内侧运动,经过最高点时对轨道压力为16mg,两球可视为质点,试求
如图,半径为R(O点为圆心,OC=R)光滑$\frac{1}{4}$圆轨道竖直放置,最高点C的切线水平,一个质量均为m的小球A沿圆轨道外侧运动,通过最高点时对轨道压力为0.75mg,另一个质量为2m 的B球沿圆轨道内侧运动,经过最高点时对轨道压力为16mg,两球可视为质点,试求 如图所示,横向宽度为L、纵向宽度足够大的区域内,直线PQ两侧分别存在强度相同、方向相反但均垂直于纸面的匀强磁场.一质量为m、电荷量为q的带正电粒子,从P点沿与PQ成θ=30°角的方向,以速度v射入下方磁场区域,粒子最终从Q点离开,不计粒子重力
如图所示,横向宽度为L、纵向宽度足够大的区域内,直线PQ两侧分别存在强度相同、方向相反但均垂直于纸面的匀强磁场.一质量为m、电荷量为q的带正电粒子,从P点沿与PQ成θ=30°角的方向,以速度v射入下方磁场区域,粒子最终从Q点离开,不计粒子重力