题目内容
10.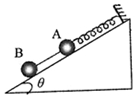 如图所示,A、B两球的质量均为m,轻质弹簧一端固定在斜面顶端,另一端与A球相连,A、B间由一轻质细线连接,倾角为θ的光滑斜面固定在地面上,弹簧、细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )
如图所示,A、B两球的质量均为m,轻质弹簧一端固定在斜面顶端,另一端与A球相连,A、B间由一轻质细线连接,倾角为θ的光滑斜面固定在地面上,弹簧、细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )| A. | B球的加速度沿斜面向下,大小为gsinθ | |
| B. | B球的加速度沿斜面向下,大小为g | |
| C. | A球的加速度沿斜面向上,大小为gsinθ | |
| D. | A球的受力情况未变,加速度为零 |
分析 初始系统处于静止状态,对系统分析,根据共点力平衡求出弹簧的弹力,烧断细线的瞬间,弹簧的弹力不变,隔离对A、B两球分析,根据牛顿第二定律求出A、B的加速度.
解答 解:AB、初始系统处于静止状态,对AB整体分析,根据共点力平衡条件知,弹簧的弹力 F弹=2mgsinθ
烧断细线瞬间,弹簧的弹力不变,对B球分析,有:mgsinθ=maB,解得 aB=gsinθ,方向沿斜面向下.故A正确,B错误.
CD、隔离对A分析,烧断细线瞬间,细线的拉力消失,受力情况发生改变,由牛顿第二定律有:F弹-mgsinθ=maA,解得 aA=gsinθ,方向沿斜面向上.故C正确,D错误.
故选:AC
点评 解决本题的关键能够正确地受力分析,抓住细线烧断的瞬间,弹簧的弹力不变,结合牛顿第二定律进行求解,掌握整体法和隔离法的运用.

练习册系列答案
相关题目
18.将一个力分解为两个分力,合力与分力的关系,下说法中错误的是( )
| A. | 合力的大小一定等于两个分力大小之和 | |
| B. | 合力的大小可能比每一个分力都大,也可能比每一个分力都小 | |
| C. | 合力的大小可能小于每一个分力的大小 | |
| D. | 合力的大小一定比一个分力大,比另一个分力小 |
5.汽车拉着拖车在水平道路上沿直线加速行驶,下列说法中正确的是( )
| A. | 汽车拉拖车的力大于拖车拉汽车的力 | |
| B. | 汽车拉拖车的力与拖车拉汽车的力大小相等 | |
| C. | 汽车拉拖车的力大于拖车受到的阻力 | |
| D. | 汽车拉拖车的力与拖车受到的阻力是一对平衡力 |
15.物体做匀加速直线运动,连续经过两段距离为8m的路程,第一段用时4s,第二段用时2s,则物体的加速度是( )
| A. | $\frac{2}{3}$m/s2 | B. | $\frac{4}{3}$m/s2 | C. | $\frac{8}{9}$m/s2 | D. | $\frac{16}{9}$m/s2 |
2.下列说法正确的是( )
| A. | 只有静止或做匀速直线运动的物体才具有惯性 | |
| B. | 作用力和反作用同时产生,同时消失 | |
| C. | 物体的运动状态发生变化,物体的受力情况一定变化 | |
| D. | 物体作曲线运动时,受到的合外力可能是恒力 |
19.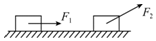 用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )
用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )
 用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )
用拉力拉同一物体由静止沿粗糙水平面运动,第一次用水平力拉,第二次用斜向上的力拉,两种情况下,物体运动的加速度相同,力作用下移动的距离也相同,则( )| A. | 两次合外力的功相同 | B. | 第一次合外力的功较大 | ||
| C. | 两次拉力的功相同 | D. | 第二次拉力的功较大 |
18.关于物体的惯性,下列说法正确的是( )
| A. | 质量就是惯性 | |
| B. | 物体的运动遵从牛顿第一定律,是因为物体有惯性 | |
| C. | 人在快速奔跑时不易被别人挡住,是因为在快速奔跑时的惯性要比走路时大 | |
| D. | 从运动的汽车上不断卸下货物,汽车的惯性不变 |
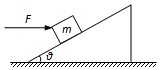 如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)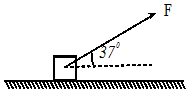 如图所示,物体的质量m=4kg,放在摩擦系数为0.25粗糙的水平面上.现在用一大小为40N力F作用在物体上,力F与水平方向的夹角为37°,使物体水平向右做匀加速直线运动运动,重力加速度g=10m/s2,已知sin37°=0.6,cos37°=0.8
如图所示,物体的质量m=4kg,放在摩擦系数为0.25粗糙的水平面上.现在用一大小为40N力F作用在物体上,力F与水平方向的夹角为37°,使物体水平向右做匀加速直线运动运动,重力加速度g=10m/s2,已知sin37°=0.6,cos37°=0.8