题目内容
8. 如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )
如图所示,三个小球a、b、c分别从三个光滑斜面顶端由静止下滑,其中a、b所在的两光滑斜面的总长度相等,高度也相同,a、c所在斜面底边相同,若球经过图上斜面转折点时无能量损失,则下列说法正确的是( )| A. | a比b后着地 | B. | a与c可能同时着地 | ||
| C. | a和b可能同时着地 | D. | a、b、c着地时速度大小可能相等 |
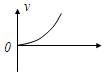
分析 这道题如采用解析法,难度很大.可以利用v-t图象(这里的v是速率,曲线下的面积表示路程s)定性地进行比较a、b两球运动时间关系.
在同一个v-t图象中作出a、b的速率图线,开始时b的加速度较大,斜率较大;由于机械能守恒,末速率相同,即曲线末端在同一水平图线上.为使路程相同(曲线和横轴所围的面积相同),显然b用的时间较少.
对于a、c,可根据牛顿第二定律和运动学公式得到时间的解析式分析.
解答 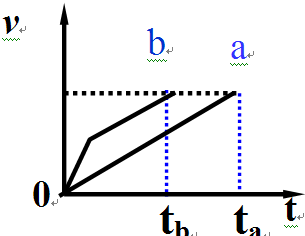 解:AC、根据机械能守恒定律得:mgh=$\frac{1}{2}m{v}_{\;}^{2}$,得 v=$\sqrt{2gh}$,可知a、b到达斜面底端时,速率相等;
解:AC、根据机械能守恒定律得:mgh=$\frac{1}{2}m{v}_{\;}^{2}$,得 v=$\sqrt{2gh}$,可知a、b到达斜面底端时,速率相等;
在同一个v-t图象中作出a、b的速率图线,显然,开始时b的加速度较大,图象的斜率较大,
由于两斜面长度相同,因此图线与t轴围成的“面积”相等.由于机械能守恒,末速率相同,即曲线末端在同一水平图线上.为使路程相同(曲线和横轴所围的面积相同),显然b用的时间较少,则a比b后着地.故A正确,C错误.
B、对于a、c,设斜面的底边长为L,斜面的倾角为α.根据牛顿第二定律得小球的加速度为:
a=$\frac{mgsinα}{m}$=gsinα
则 $\frac{L}{cosα}$=$\frac{1}{2}a{t}_{\;}^{2}$
联立解得:t=2$\sqrt{\frac{L}{gsin2α}}$,则知a与c运动的时间可能相等,(如C斜面倾角30°,a斜面倾角为60°)可能同时着地.故B正确.
D、由上分析知,由机械能守恒定律知,a、b着地时速度大小相等,大于c的速度.故D错误.
故选:AB
点评 利用图象描述物理过程更直观 物理过程可以用文字表述,也可用数学式表达,还可以用物理图象描述.而从物理图象上可以更直观地观察出整个物理过程的动态特征.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 电流 | B. | 电压 | C. | 电容 | D. | 电场强度 |
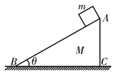
| A. | m可能是向下做加速运动 | |
| B. | 地面对木楔的支持力一定大于(M+m)g | |
| C. | 地面对木楔的摩擦力一定水平向右 | |
| D. | m对木楔作用力的水平分量小于地面对木楔的摩擦力 |
| A. | 合力的大小一定等于两个分力大小之和 | |
| B. | 合力的大小可能比每一个分力都大,也可能比每一个分力都小 | |
| C. | 合力的大小可能小于每一个分力的大小 | |
| D. | 合力的大小一定比一个分力大,比另一个分力小 |

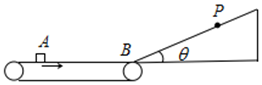 如图所示,足够长的浅色传送带以速度v0=8m/s顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量m=1kg的墨色小滑块从距离B点s0=10m的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为μ1=0.4,斜面倾角θ=37°,斜面足够长,滑块与斜面的动摩擦因数μ2=0.45,重力加速度g=10m/s2,sin37°=0.6cos37°=0.8,求:
如图所示,足够长的浅色传送带以速度v0=8m/s顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量m=1kg的墨色小滑块从距离B点s0=10m的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为μ1=0.4,斜面倾角θ=37°,斜面足够长,滑块与斜面的动摩擦因数μ2=0.45,重力加速度g=10m/s2,sin37°=0.6cos37°=0.8,求: 如图所示,倾角θ=37°的粗糙斜面固定在水平面上,质量m=2.0kg的物块(可视为质点),在沿斜面向上的拉力F作用下,由静止开始从斜面底端沿斜面向上运动.已知拉力F=32N,物块与斜面间的动摩擦因数为μ=0.25,sin37°=0.6,cos37°=0.8,且斜面足够长.取重力加速度g=10m/s2,求:
如图所示,倾角θ=37°的粗糙斜面固定在水平面上,质量m=2.0kg的物块(可视为质点),在沿斜面向上的拉力F作用下,由静止开始从斜面底端沿斜面向上运动.已知拉力F=32N,物块与斜面间的动摩擦因数为μ=0.25,sin37°=0.6,cos37°=0.8,且斜面足够长.取重力加速度g=10m/s2,求: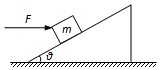 如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,斜面体固定在粗糙水平地面上,斜面倾角为θ=37°,质量为m=2kg的物体在水平向右的推力F=40N作用下恰好能沿斜面向上匀速运动.(sin37°=0.6,cos37°=0.8,g=10m/s2)