题目内容
(10分)如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。已知物体A、B的质量相等均为M,,轻绳与轻滑轮间的摩擦不计,轻绳不可伸长且足够长,求: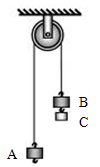
(1)若物体C的质量为M/4,物体B从静止开始下落一段距离的时间与自由落体下落同样的距离所用时间的比值。
(2)如果连接AB的轻绳能承受的最大拉力为1.2Mg,那么对物体C的质量有何要求?
(1)3:1;(2) m≤0.5Mg
解析试题分析:(1)设滑轮两侧物体运动的加速度大小为a ,绳的张力为T,B下落距离h用时为t1;自由下落距离h用时为t2.
根据牛顿第二定律 研究A: 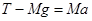
研究BC: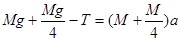
根据运动学公式 :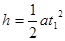
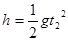
代入数据联立解得: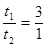
(2)设物体C的质量为m根据牛顿第二定律
研究A: 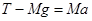
研究BC: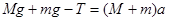
令T≤1.2Mg ,解得m≤0.5Mg
考点:牛顿第二定律的应用。

练习册系列答案
相关题目
如图甲所示,用一水平外力F推着一个静止在倾角为 的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10 m/s2。根据图乙中所提供的信息可以计算出(
的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10 m/s2。根据图乙中所提供的信息可以计算出( )
)
| A.物体的质量 |
| B.物体能静止在斜面上所施加的外力 |
| C.斜面的倾角 |
| D.加速度为6 m/s2时物体的速度 |


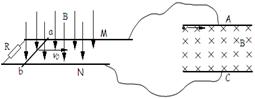
 ,不计一切摩擦和阻力。求:
,不计一切摩擦和阻力。求: