题目内容
如图所示,轻绳的一端固定在O点,另一端系一质量为m的小球(可视为质点)。当小球在竖直平面内沿逆时针方向做圆周运动时,通过传感器测得轻绳拉力T、轻绳与竖直线OP的夹角θ满足关系式T=a+bcosθ,式中a、b为常数。若不计空气阻力,则当地的重力加速度为( )
A. | B. | C. | D. |
D
解析试题分析:在最高点时:设此时物体的速度为V1,由题意可知:θ=1800,绳的拉力T1=a-b;
根据向心力公式有: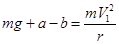
在最低点时:设此时物体的速度为V2,由题意可知:θ=00,绳的拉力T1=a+b;
根据向心力公式有:
只有重力做功,由机械能守恒定律:
解得: ;所以D正确。
;所以D正确。
考点: 向心力公式,机械能守恒定律。

如图所示,固定的倾斜光滑杆上套有一个质量为m的小球,小球与一轻质弹簧一端相连,弹簧的另一端固定在地面上的A点,已知杆与水平面之间的夹角θ<45°,当小球位于B点时,弹簧与杆垂直,此时弹簧处于原长。现让小球自C点由静止释放,在小球滑到杆底端的整个过程中,关于小球的动能、重力势能和弹簧的弹性势能,下列说法正确的是
| A.小球的动能与重力势能之和保持不变 |
| B.小球的动能与重力势能之和先增大后减少 |
| C.小球的动能与弹簧的弹性势能之和保持不变 |
| D.小球的重力势能与弹簧的弹性势能之和保持不变 |
如图所示,一根跨越一固定水平光滑细杆的轻绳,两端各系一个小球,球a置于地面,球b被拉到与细杆同一水平的位置。在绳刚被拉直时,球b从静止状态向下摆动,当球b摆到竖直位置时,球a刚要离开地面,则两球质量之比ma : mb为( )
| A.4 | B.3 | C.2 | D.1 |
如图所示,质量为m的小球固定于轻质弹簧的一端,弹簧的另一端固定于O点,将小球拉至A处,弹簧恰好无形变。由静止释放小球,它运动到O点正下方B点间的竖直高度差为h,速度为v。下列说法正确的是
| A.由A到B小球的机械能减少 |
| B.由A到B重力势能减少mv2/2 |
| C.由A到B小球克服弹力做功为mgh |
| D.小球到达B时弹簧的弹性势能为mgh-mv2/2 |
如图所示,斜面置于光滑水平地面上,其光滑斜面上有一物体由静止沿斜面下滑,在物体下滑过程中,下列说法正确的是
| A.物体的重力势能减少,动能增加,机械能减小 |
| B.斜面的机械能不变 |
| C.斜面对物体的作用力垂直于接触面,不对物体做功 |
| D.物体和斜面组成的系统机械能守恒 |
如图,两个半径均为R的1/4光滑圆弧对接于O点,有物体从上面圆弧的某点C以上任意位置由静止下滑(C点未标出),都能从O点平抛出去,则
| A.∠CO1O=60° |
| B.∠CO1O=45° |
| C.落地点距O2最远为2R |
| D.落地点距O2最近为R |
如图所示,从光滑的1/ 4圆弧槽的最高点滑下的小滑块,滑出槽口时速度方向为水平方向,槽口与一个半球顶点相切,半球底面为水平,若要使小物块滑出槽口后不沿半球面下滑,已知圆弧轨道的半径为R1,半球的半径为R2,则R1和R2应满足的关系是
| A.R1≤R2/2 |
| B.R1≥R2/2 |
| C.R1≤R2 |
| D.R1≥R2 |

