Question

16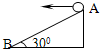．如图，AB为斜面，倾角为30°，小球从A点以初速度v₀水平抛出，恰好落到B点．求：
（1）AB间的距离；
（2）小球与斜面间的最大距离．

Answer 1

分析 根据竖直位移和水平位移的关系求出平抛运动的时间，根据水平位移的大小，结合平行四边形定则求出AB间的距离．
将小球的运动分解为沿斜面方向和垂直斜面方向，抓住垂直斜面方向上的初速度和加速度，结合速度位移公式求出小球与斜面间的最大距离．

解答 解：（1）根据$tan30°=\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$得，t=$\frac{2{v}_{0}tan30°}{g}$，
则AB间的距离s=$\frac{{v}_{0}t}{cos30°}=\frac{2{{v}_{0}}^{2}tan30°}{gcos30°}$=$\frac{4{{v}_{0}}^{2}}{3g}$．
（2）将小球的运动分解为沿斜面方向和垂直斜面方向，在垂直斜面方向上的分速度v_y=v₀sin30°，加速度a_y=gcos30°，
则小球与斜面间的最大距离d=$\frac{{{v}_{y}}^{2}}{2a}=\frac{\frac{{{v}_{0}}^{2}}{4}}{2g×\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}{{v}_{0}}^{2}}{12g}$．
答：（1）AB间的距离为$\frac{4{{v}_{0}}^{2}}{3g}$；
（2）小球与斜面间的最大距离为$\frac{{\sqrt{3}v_0^2}}{12g}$．

点评 解决本题的关键掌握处理平抛运动的方法，在第一问中，将平抛运动分解为水平方向和竖直方向进行求解，第二问中，将平抛运动分解为沿斜面方向和垂直斜面方向分析求解．