题目内容
2.随着科技的发展,可以对宇宙中越来越多的星体进行研究,质量为1kg的探测器,在距某星球球心4.0×105km处绕其做匀速圆周运动,周期为2.0×105s,已知地球半径为6.4×108km,表面重力加速度g=9.8m/s2,则该星球的质量与地球的质量之比约为( )| A. | 102 | B. | 105 | C. | 104 | D. | 108 |
分析 探测器绕星球做匀速圆周运动,根据万有引力提供向心力求星球质量;地球表面物体重力等于万有引力求出地球质量,最后求两者的比值.
解答 解:探测器绕星球做匀速圆周运动,根据万有引力提供向心力有:
$G\frac{{M}_{星}^{\;}m}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
解得星球质量${M}_{星}^{\;}=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$
地球表面物体质量等于万有引力mg=$G\frac{Mm}{{R}_{\;}^{2}}$
解得:$M=\frac{g{R}_{\;}^{2}}{G}$
$\frac{{M}_{星}^{\;}}{M}=\frac{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}}{\frac{g{R}_{\;}^{2}}{G}}$=$\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{g{T}_{\;}^{2}{R}_{\;}^{2}}$=$\frac{4×10×(4.0×1{0}_{\;}^{8})_{\;}^{3}}{9.8×(2.0×1{0}_{\;}^{5})_{\;}^{2}×(6.4×1{0}_{\;}^{11})_{\;}^{2}}$=$1{0}_{\;}^{2}$
故选:A
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
相关题目
12. 图示电路中,变压器为理想变压器,a、b接在电压有效值不变的交流电源两端,R0为定值电阻,R为滑动变阻器.现将变阻器的滑片从一个位置滑动到另一位置,观察到电流表A1的示数增大了0.2A,电流表A2的示数增大了0.8A,则下列说法正确的是( )
图示电路中,变压器为理想变压器,a、b接在电压有效值不变的交流电源两端,R0为定值电阻,R为滑动变阻器.现将变阻器的滑片从一个位置滑动到另一位置,观察到电流表A1的示数增大了0.2A,电流表A2的示数增大了0.8A,则下列说法正确的是( )
 图示电路中,变压器为理想变压器,a、b接在电压有效值不变的交流电源两端,R0为定值电阻,R为滑动变阻器.现将变阻器的滑片从一个位置滑动到另一位置,观察到电流表A1的示数增大了0.2A,电流表A2的示数增大了0.8A,则下列说法正确的是( )
图示电路中,变压器为理想变压器,a、b接在电压有效值不变的交流电源两端,R0为定值电阻,R为滑动变阻器.现将变阻器的滑片从一个位置滑动到另一位置,观察到电流表A1的示数增大了0.2A,电流表A2的示数增大了0.8A,则下列说法正确的是( )| A. | 变阻器滑片是沿c→d的方向滑动 | B. | 电压表V1示数增大 | ||
| C. | 电压表V2、V3示数均增大 | D. | 该变压器起升压作 |
13.如图甲所示为一列沿x轴传播的简谐横波某时刻的图象,已知从该时刻起,图中质点A的振动图象如图乙所示,图中的质点B第一次经过平衡位置所需的时间大于0.1s,则下列说法中正确的是( )


| A. | 波沿x轴负方向传播 | |
| B. | t=0.3 s时,质点A沿x轴方向运动了1.5m | |
| C. | t=0.2 s时,质点B的加速度方向沿y轴正方向 | |
| D. | 质点B的振动频率为0.4Hz |
10.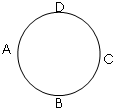 粗细均匀的金属环上A、B、C、D四点把其周长分成四等分,如图所示.则A、B间与A、C间电阻之比为( )
粗细均匀的金属环上A、B、C、D四点把其周长分成四等分,如图所示.则A、B间与A、C间电阻之比为( )
 粗细均匀的金属环上A、B、C、D四点把其周长分成四等分,如图所示.则A、B间与A、C间电阻之比为( )
粗细均匀的金属环上A、B、C、D四点把其周长分成四等分,如图所示.则A、B间与A、C间电阻之比为( )| A. | 1:3 | B. | 1:2 | C. | 3:4 | D. | 4:3 |
7.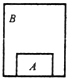 如图,物体A静止在箱子B中,离地足够高,某时刻将它们由静止自由释放,则在下落过程中,下列说法正确的是( )
如图,物体A静止在箱子B中,离地足够高,某时刻将它们由静止自由释放,则在下落过程中,下列说法正确的是( )
 如图,物体A静止在箱子B中,离地足够高,某时刻将它们由静止自由释放,则在下落过程中,下列说法正确的是( )
如图,物体A静止在箱子B中,离地足够高,某时刻将它们由静止自由释放,则在下落过程中,下列说法正确的是( )| A. | 若没有空气阻力,A开始的一段短时间内,速度增加得越来越快 | |
| B. | 若没有空气阻力,A所受的支持力始终为零 | |
| C. | 若空气阻力与速度成正比,则开始的一段短时间内,A受的支持力越来越大 | |
| D. | 若空气阻力与速度成正比,只要下落时间足够长,则A可能不受B的支持力而“飘”起来 |
11.关于电阻率,下列说法中不正确的是( )
| A. | 所谓超导体,当其温度降低到接近绝对零度的某个临界温度时,电阻率突然变为零 | |
| B. | 各种材料的电阻率都与温度有关,金属的电阻率随温度升高而增大 | |
| C. | 电阻率是表征材料导电性能好坏的物理量,电阻率越大,其导电性能越好 | |
| D. | 某些合金的电阻率几乎不受温度变化的影响,通常都用它们制作标准电阻 |
12.两物体组成的系统总动量守恒,这个系统中( )
| A. | 一个物体增加的速度等于另一个物体减少的速度 | |
| B. | 一物体受的冲量与另一物体所受冲量相同 | |
| C. | 两个物体的动量变化总是大小相等,方向相同 | |
| D. | 系统总动量的变化为零 |