题目内容
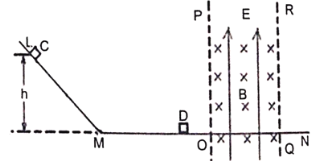
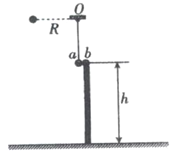
【题目】如图所示，一个质量为m1=2kg的小球a用一根长为R=1.25m的轻绳悬挂于O点静止。小球a的右侧水平地面上有一竖立支架，支架上放置另一小球b，两小球刚好接触但之间无弹力，且两球球心在同一水平线上，小球b的质量为m2=4kg，支架高h=3.2m。现把小球a拉至左侧与O点等高处，此时轻绳刚好拉直，然后由静止释放球a，到达最低点时两球相碰，碰后球a向左做圆周运动，上升的最大高度为h′=0.05m。小球b碰后的瞬间立即受到一个大小F=20N的水平向右恒力。取g=10m/s2。求：
(1)碰撞前后的瞬间轻绳的弹力大小之比；
(2)球b着地时的动能。
【答案】（1）
；（2）
【解析】
解：(1)碰撞前后瞬间球a的速度大小分别为
、
，根据机械能守恒有：
碰撞前：
碰撞后：
根据牛顿运动定律得碰撞前瞬间：
碰撞后瞬间：
联立解得：
(2两小球碰撞过程，根据动量守恒定律有：
解得：
小球b碰撞后，竖直方向上做自由落体运动，有：
，
解得：
，
水平方向上球b碰后在恒力作用下做匀加速直线运动，根据牛顿运动定律有：
根据运动学公式，有：
球b着地时的速度为：
球b着地时的动能为：
解得：
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
