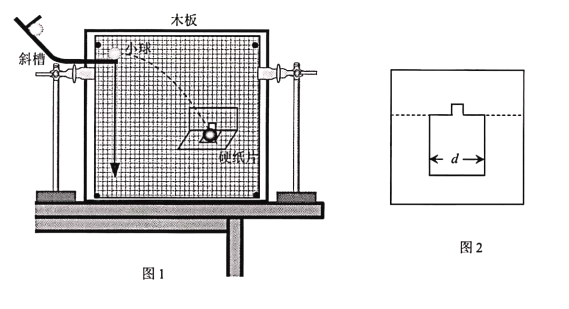
题目内容
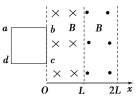
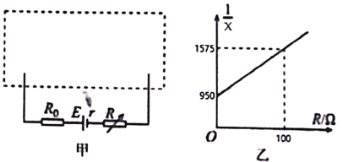
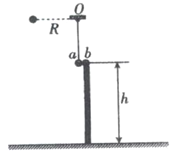
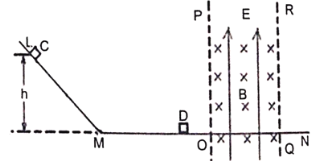
【题目】固定在竖直平面内的光滑绝缘轨道LMN,其中M水平且足够长,LM下端与MN平滑相接。在OP与QR之间的区域内有方向如图所示的匀强电场和匀强磁场。质量为m和5m的绝缘小物块C、D(可视为质点),其中D带有一定电荷量q,C不带电,现将物块D静止放置在水平轨道的MO段,将物块C从离水平轨道MN距离h高的L处由静止释放,物块C沿轨道下滑进入水平轨道,然后与D正碰(C、D的电荷量都不变),碰后物块C被反弹,物块D进入虚线OP右侧的复合场中沿直线OQ运动且恰好对水平轨道无压力,最后离开复合场区域。已知:重力加速度g、电场强度E=![]() 、磁感应强度B=
、磁感应强度B=![]() ,求:
,求:
(1)物块D进入电磁场的速度大小;
(2)物块C反弹后滑回斜面LM的最大高度H;
(3)若已知OQ间距为h,保持其他条件不变,仅将电场强度增大为E2=5E,同时磁感应强度减小为B2=![]() ,那么物块D离开电磁场后所到达轨迹最高点离水平轨道MN的高度?
,那么物块D离开电磁场后所到达轨迹最高点离水平轨道MN的高度?
【答案】(1)![]() (2)
(2)![]() (3)0.44h
(3)0.44h
【解析】
.(1)对物块C在斜面上L→M的过程有 ![]()
即 ![]()
对物块D进入电磁场后做匀速直线运动可知 D带正电, 且![]()
解得![]()
(2)C碰D 动量守恒 ![]()
解得 ![]()
物块C返回斜面有![]()
解得![]()
(3)物块D在电磁场中![]() ,重力与静电力平衡,做匀速圆周运动
,重力与静电力平衡,做匀速圆周运动
有![]()
圆周运动半径![]()
在有界场中轨迹为运动的圆心角为θ, ![]()
![]() 从Q点正上方处离开电磁场。
从Q点正上方处离开电磁场。
物块D离开磁场后作曲线运动,竖直速度为 ![]()
则 ![]()
物块D离开电磁场后所到达轨迹最高点离水平轨道MN的高度为
H=h1+h2=0.44h

练习册系列答案
相关题目