Question

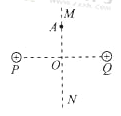
【题目】如图所示，竖直线MN左侧存在水平向右的匀强电场，右侧存在垂直纸面向外的匀强磁场其磁感应强度大小B=π×10－2T，在P点竖直下方， m处有一垂直于MN的足够大的挡板。现将一重力不计、比荷=1×106C/kg的正电荷从P点由静止释放，经过△t=1×10－4s，电荷以v0=1×104m/s的速度通过MN进入磁场。求：

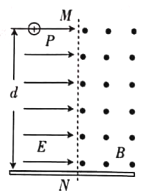
(1)P点到MN的距离及匀强电场的电场强度E的大小；

(2)电荷打到挡板的位置到MN的距离；

(3)电荷从P点出发至运动到挡板所用的时间。

Answer 1

【答案】（1）0.5m；100N/C（2）0.28m（3）4.67×10-4s

【解析】

（1）根据平均速度公式求解P点到MN的距离；根据牛顿第二定律结合运动公式求解匀强电场的电场强度E的大小；

（2）电荷在磁场中做匀速圆周运动，画出运动的轨迹，结合结合关系求解电荷打到挡板的位置到MN的距离；

（3）根据几何关系求解电荷在磁场中运动的圆弧所对的圆心角，根据求解时间；根据运动公式求解在电场中的运动时间.

（1）电荷在电场中做匀加速直线运动，P点到MN的距离为

解得x=0.5m

由速度公式v0=at

由牛顿第二定律qE=ma

解得E=100N/C

（2）电荷在电场中做匀速圆周运动，由牛顿第二定律可得：

解得

运动周期

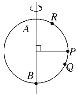
电荷在电场、磁场中的运动轨迹如图，

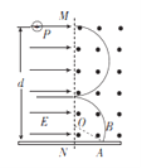
Q点到挡板的距离为

则，即

A点到MN的距离x=rcos600=m=0.28m.

（3）电荷在电场中运动的总时间：

电荷在磁场中运动的圆弧所对的圆心角为

电荷在磁场中运动的总时间

解得

则电荷从P点出发至运动到挡板所需的时间为