题目内容
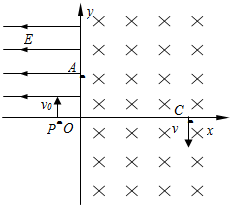
如图表示,在磁感强度为B的水平匀强磁场中,有一足够长的绝缘细棒OO′在竖直面内垂直磁场方向放置,细棒与水平面夹角为α.一质量为m、带电荷为+q的圆环A套在OO′棒上,圆环与棒间的动摩擦因数为μ,且μ<tanα.现让圆环A由静止开始下滑,试问圆环在下滑过程中:
(1)圆环A的最大加速度为多大?获得最大加速度时的速度为多大?
(2)圆环A能够达到的最大速度为多大?

(1)圆环A的最大加速度为多大?获得最大加速度时的速度为多大?
(2)圆环A能够达到的最大速度为多大?

(1)由于μ<tanα,所以环将由静止开始沿棒下滑.环A沿棒运动的速度为v1时,受到重力mg、洛仑兹力qv1B、杆的弹力N1和摩擦力f1=μN1.
根据牛顿第二定律,对沿棒的方向有mgsinα-f1=ma
垂直棒的方向有N1+qv1B=mgcosα
所以当f1=0,即N1=0时,a有最大值am,且am=gsinα
此时qv1B=mgcosα
解得v1=
(2)设当环A的速度达到最大值vm时,环受杆的弹力为N2,方向垂直于杆向下,摩擦力为f2=μN2.此时应有a=0,即
mgsinα=f2
N2+mgcosα=qvmB
解得vm=
答:
(1)圆环A的最大加速度为gsinα,获得最大加速度时的速度为
.
(2)圆环A能够达到的最大速度为
.

根据牛顿第二定律,对沿棒的方向有mgsinα-f1=ma
垂直棒的方向有N1+qv1B=mgcosα
所以当f1=0,即N1=0时,a有最大值am,且am=gsinα
此时qv1B=mgcosα
解得v1=
| mgcosα |
| qB |
(2)设当环A的速度达到最大值vm时,环受杆的弹力为N2,方向垂直于杆向下,摩擦力为f2=μN2.此时应有a=0,即
mgsinα=f2
N2+mgcosα=qvmB
解得vm=
| mg(sinα+μcosα) |
| μqB |
答:
(1)圆环A的最大加速度为gsinα,获得最大加速度时的速度为
| mgcosα |
| qB |
(2)圆环A能够达到的最大速度为
| mg(sinα+μcosα) |
| μqB |


练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目