题目内容
随着航天技术的发展,在地球周围有很多人造飞行器,其中有一些已超过其设计寿命且能量耗尽。每到太阳活动期,地球的大气层会变厚,这时有些飞行器在大气阻力的作用下,运行的轨道高度将逐渐降低(在其绕地球运动的每一周过程中,轨道高度变化很小,均可近似视为匀速圆周运动)。为了避免飞行器坠入大气层后对地面设施及人员造成安全威胁,人们设想发射导弹将其在运行轨道上击碎。具体设想是:在导弹的弹头脱离推进装置后,经过一段无动力飞行,从飞行器后下方逐渐接近目标,在进入有效命中距离后引爆弹头并将该飞行器击碎。对于这一过程中的飞行器及弹头,下列说法中正确的是( )
| A.飞行器轨道高度降低后,它做圆周运动的速率变大 |
| B.飞行器轨道高度降低后,它做圆周运动的周期变大 |
| C.弹头在脱离推进装置之前,始终处于失重状态 |
| D.弹头引爆前瞬间,弹头的加速度一定小于此时飞行器的加速度 |
A
解析试题分析:飞行器做圆周运动,万有引力充当向心力,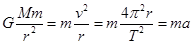 ,解得v=
,解得v=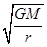 ,T=2
,T=2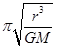 ,a=
,a=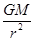 ,随高度降低,v增大,T减小,a增大,故选项A正确B错误,因弹头引爆前比飞行器高度要低,故加速度大,选项D也错误;弹头脱离推进装置前,在推力作用下具有向上的加速度,故处于超重状态,选项C错误。
,随高度降低,v增大,T减小,a增大,故选项A正确B错误,因弹头引爆前比飞行器高度要低,故加速度大,选项D也错误;弹头脱离推进装置前,在推力作用下具有向上的加速度,故处于超重状态,选项C错误。
考点:万有引力定律 牛顿第二定律 超失重

 暑假作业暑假快乐练西安出版社系列答案
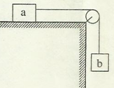
暑假作业暑假快乐练西安出版社系列答案如图所示,静止在光滑水平面上的物体A,一端靠着处于自然状态的弹簧.现对物体作用一水平恒力,在弹簧被压缩到最短的过程中,物体的速度和加速度的变化情况是 
| A.速度增大,加速度增大 |
| B.速度增大,加速度减小 |
| C.速度先增大后减小,加速度先增大后减小 |
| D.速度先增大后减小,加速度先减小后增大 |
如图所示:质量为m的木块与质量为M的长木板一起以初速度v在地面上滑行,仅在摩擦力作用下做匀减速直线运动,滑行过程中二者始终相对静止,长木板与地面间动摩擦因数为 ,木块与长木板间动摩擦因数为
,木块与长木板间动摩擦因数为 ,则滑行过程中木块受到的摩擦力一定为( )
,则滑行过程中木块受到的摩擦力一定为( )
| A.μ1(m+M)g | B.μ2mg |
| C.μ1mg | D.μ1mg+μ2Mg |
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端,B与小车平板间的动摩擦因数为μ,若细线偏离竖直方向θ角,则小车对物块B产生的作用力的大小和方向为
| A.mg,竖直向上 | B.mg ,斜向左上方 ,斜向左上方 |
| C.mgtanθ,水平向右 | D.mg ,斜向右上方 ,斜向右上方 |
如图所示,质量为M=5kg的箱子B置于光滑水平面上,箱子底板上放一质量为m2=1kg的物体C,质量为m1=2kg的物体A经跨过定滑轮的轻绳与箱子B相连,在A加速下落的过程中,C与箱子B始终保持相对静止。不计定滑轮的质量和一切阻力,取g=10m/s2,下列不正确的是( )
| A.物体A处于失重状态 |
| B.物体A的加速度大小为2.5m/s2 |
| C.物体C对箱子B的静摩擦力大小为2.5N |
| D.轻绳对定滑轮的作用力大小为30N |
如图所示,倾角为 的光滑斜面下端固定一绝缘轻弹簧,M点固定一个质量为m、带电量为-q的小球Q。整个装置处在场强大小为E、方向沿斜面向下的匀强电场中。现把一个带电量为+q的小球P从N点由静止释放,释放后P沿着斜面向下运动。N点与弹簧的上端和M的距离均为s0。P、Q以及弹簧的轴线ab与斜面平行。两小球均可视为质点和点电荷,弹簧的劲度系数为k0,静电力常量为k。则( )
的光滑斜面下端固定一绝缘轻弹簧,M点固定一个质量为m、带电量为-q的小球Q。整个装置处在场强大小为E、方向沿斜面向下的匀强电场中。现把一个带电量为+q的小球P从N点由静止释放,释放后P沿着斜面向下运动。N点与弹簧的上端和M的距离均为s0。P、Q以及弹簧的轴线ab与斜面平行。两小球均可视为质点和点电荷,弹簧的劲度系数为k0,静电力常量为k。则( )
| A.小球P返回时,不可能撞到小球Q |
B.小球P在N点的加速度大小为 |
| C.小球P沿着斜面向下运动过程中,其电势能一定减少 |
D.当弹簧的压缩量为 时,小球P的速度最大 时,小球P的速度最大 |

 B.
B.
 D.
D.
