题目内容
如图所示，带支架的平板小车沿水平面向左做直线运动，小球A用细线悬挂于支架前端，质量为m的物块B始终相对于小车静止地摆放在右端，B与小车平板间的动摩擦因数为μ，若细线偏离竖直方向θ角，则小车对物块B产生的作用力的大小和方向为
| A．mg，竖直向上 | B．mg ，斜向左上方 |
| C．mgtanθ，水平向右 | D．mg ，斜向右上方 |
D
解析试题分析：以A为研究对象，由受力图，根据牛顿第二定律得： mAgtanθ=mAa，得a=gtanθ，方向水平向右．再对B研究得：小车对B的摩擦力f=ma=mgtanθ，方向水平向右，小车对B的支持力大小为N=mg，方向竖直向上，则小车对物块B产生的作用力的大小为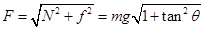
，方向斜向右上方，故选D。
考点：牛顿第二定律的应用。
世纪百通期末金卷系列答案如图所示，A是半径为r的圆形光滑轨道，固定在木板B上，竖直放置；B的左右两侧各有一光滑挡板固定在地面上，使其不能左右运动，小球C静止放在轨道最低点，A，B，C质量相等。现给小球一水平向右的初速度v0，使小球在圆型轨道的内侧做圆周运动，为保证小球能通过轨道的最高点，且不会使B离开地面，初速度v0必须满足（ ）（重力加速度为g）
A．最小值为 | B．最大值为 |
C．最小值为 | D．最大值为 |
关于运动和力，下列说法中正确的是（ ）
| A．物体运动速度变化越快，加速度越大 |
| B．做直线运动的物体受到的合外力一定是恒力 |
| C．做匀速圆周运动的物体的加速度不变 |
| D．做平抛运动的物体在任意一段时间内速度变化的方向是不相同的 |
如图所示，半径为R的金属环竖直放置，环上套有一质量为m的小球，小球开始时静止于最低点。现给小球一冲击，使它以初速度
。小球运动到环的最高点时与环恰无作用力，小球从最低点运动到最高点的过程中（ ）
| A．小球机械能守恒 |
| B．小球在最低点时对金属环的压力是6mg |
C．小球在最高点时，重力的功率是 |
| D．小球机械能不守恒，且克服摩擦力所做的功是0 5mgR。 |
如图甲所示，平行于斜面的轻弹簧，劲度系数为 k，一端固定在在倾角为θ的斜面底端，另一端与Q物块连接，P、Q质量均为m，斜面光滑且固定在水平面上，初始时物块均静止．现用平行于斜面向上的力F拉物块P，使P做加速度为a 的匀加速运动，两个物块在开始一段时间内的
图象如图乙所示（重力加速度为g），则下列说法不正确的是( )
| A．平行于斜面向上的拉力F一直增大 |
| B．外力施加的瞬间，P、Q间的弹力大小为m（gsinθ—a） |
C．从O开始到t1时刻，弹簧释放的弹性势能为 mv12 |
| D．t2时刻弹簧恢复到原长，物块Q达到速度最大值 |
如图所示，质量为m=1kg的物体与水平地面之间的动摩擦因数为0.3，当物体运动的速度为10m／s时，给物体施加一个与速度方向相反的大小为F=2N的恒力，在此恒力作用下(取g=10m／s2)（ ）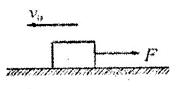
| A．物体经10s速度减为零 |
| B．物体经5s速度减为零 |
| C．物体速度减为零后将保持静止 |
| D．物体速度减为零后将向右运动 |
随着航天技术的发展，在地球周围有很多人造飞行器，其中有一些已超过其设计寿命且能量耗尽。每到太阳活动期，地球的大气层会变厚，这时有些飞行器在大气阻力的作用下，运行的轨道高度将逐渐降低（在其绕地球运动的每一周过程中，轨道高度变化很小，均可近似视为匀速圆周运动）。为了避免飞行器坠入大气层后对地面设施及人员造成安全威胁，人们设想发射导弹将其在运行轨道上击碎。具体设想是：在导弹的弹头脱离推进装置后，经过一段无动力飞行，从飞行器后下方逐渐接近目标，在进入有效命中距离后引爆弹头并将该飞行器击碎。对于这一过程中的飞行器及弹头，下列说法中正确的是（ ）
| A．飞行器轨道高度降低后，它做圆周运动的速率变大 |
| B．飞行器轨道高度降低后，它做圆周运动的周期变大 |
| C．弹头在脱离推进装置之前，始终处于失重状态 |
| D．弹头引爆前瞬间，弹头的加速度一定小于此时飞行器的加速度 |
如图所示，轻质弹簧的一端与固定的竖直板P拴接，另一端与物体A相连，物体A置于光滑水平桌面上，A右端连接一细线，细线绕过光滑的定滑轮与物体B相连。开始时托住B，让A处于静止且细线恰好伸直，然后由静止释放B，直至B获得最大速度。下列有关该过程的分析中正确的是（ ）
| A．B物体受到细线的拉力保持不变 |
| B．B物体机械能的减少量大于弹簧弹性势能的增加量 |
| C．A物体动能的增量等于B物体重力对B做的功与弹簧弹力对A做的功之和 |
| D．A物体与弹簧所组成的系统机械能的增加量等于细线拉力对A做的功 |
如图所示，用力F推放在光滑水平面上的物体P、Q、R，使其做匀加速运动. 若P和Q之间的相互作用力为6 N，Q和R之间的相互作用力为4 N，Q的质量是2 kg，那么R的质量是（ ）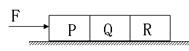
| A．2 kg | B．3 kg | C．4 kg | D．5 kg |