题目内容
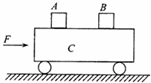 如图所示,质量分别为mA=0.4kg和mB=0.6kg的可视为质点的A、B两物体,放在质量为mC=1kg的足够长的小车C上.A、B相距L=12.5cm,它们随车以v0=1.0m/s的速度在光滑的水平面上向右匀速运动.若在小车上加一水平向右的推力F=3.8N,A、B便在小车上滑动.已知A、B与小车间的动摩擦因数分别为μA=0.2,μB=0.1,(g取10m/s2.)
如图所示,质量分别为mA=0.4kg和mB=0.6kg的可视为质点的A、B两物体,放在质量为mC=1kg的足够长的小车C上.A、B相距L=12.5cm,它们随车以v0=1.0m/s的速度在光滑的水平面上向右匀速运动.若在小车上加一水平向右的推力F=3.8N,A、B便在小车上滑动.已知A、B与小车间的动摩擦因数分别为μA=0.2,μB=0.1,(g取10m/s2.)(1)试求经过多长时间A、B两物体在车上相碰?
(2)碰前瞬间三物体的速度VA、VB、VC分别是多少?
(3)若在A、B相碰前的瞬间撤去推力F,碰后和C的速度分别变成了 VA′=0.95m/s、VB′=2.2m/s和 VC′=2.2m/s.此时A、B距小车左端15厘米远,问A物体能否从小车C上滑下?
分析:(1)根据牛顿第二定律分别求出A、B的加速度,结合位移关系求出A、B两物体在车上相碰经历的时间.
(2)根据牛顿第二定律求出C的加速度,结合运动学公式求出碰前瞬间三物体的速度大小.
(3)假设A不滑下,结合动量守恒定律和能量守恒定律求出A相对滑动的距离,从而判断出A能否从小车上滑下.
(2)根据牛顿第二定律求出C的加速度,结合运动学公式求出碰前瞬间三物体的速度大小.
(3)假设A不滑下,结合动量守恒定律和能量守恒定律求出A相对滑动的距离,从而判断出A能否从小车上滑下.
解答:解:(1)A的加速度aA=
=μAg=2m/s2.
B的加速度aB=
=μBg=1m/s2.
根据v0t+
aAt2-v0t-
aBt2=L,
代入数据解得t=0.5s.
(2)碰前A的速度vA=v0+aAt=1+2×0.5m/s=2m/s.
碰前B的速度vB=v0+aBt=1+1×0.5m/s=1.5m/s.
C的加速度aC=
=
m/s2=2.4m/s2.
则碰前C的速度vC=v0+act=1+2.4×0.5m/s=2.2m/s.
(3)碰后BC的速度相同,保持相对静止,根据动量守恒定律得,
mAvA′+(mB+mC)vB′=(mA+mB+mC)v
代入数据解得v=1.95m/s.
根据能量守恒知,μ AmAgs相对=
mAvA′2+
(mB+mC)vB′2-
(mA+mB+mC)v2
代入数据解得,s相对=0.3125m=31.25cm>15cm,知A能从小车上滑下.
答:(1)经过0.5s时间A、B两物体在车上相碰.
(2)碰前瞬间三物体的速度VA、VB、VC分别是2m/s、1.5m/s、2.2m/s.
(3)A能从小车上滑下.
| μAmAg |
| mA |
B的加速度aB=
| μBmBg |
| mB |
根据v0t+
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得t=0.5s.
(2)碰前A的速度vA=v0+aAt=1+2×0.5m/s=2m/s.
碰前B的速度vB=v0+aBt=1+1×0.5m/s=1.5m/s.
C的加速度aC=
| F-μ AmAg-μBmBg |
| mC |
| 3.8-0.2×4-0.1×6 |
| 1 |
则碰前C的速度vC=v0+act=1+2.4×0.5m/s=2.2m/s.
(3)碰后BC的速度相同,保持相对静止,根据动量守恒定律得,
mAvA′+(mB+mC)vB′=(mA+mB+mC)v
代入数据解得v=1.95m/s.
根据能量守恒知,μ AmAgs相对=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
代入数据解得,s相对=0.3125m=31.25cm>15cm,知A能从小车上滑下.
答:(1)经过0.5s时间A、B两物体在车上相碰.
(2)碰前瞬间三物体的速度VA、VB、VC分别是2m/s、1.5m/s、2.2m/s.
(3)A能从小车上滑下.
点评:本题分析物体的运动情况是解题的关键,运用牛顿第二定律、运动学和动量守恒进行求解.

练习册系列答案
相关题目
 如图所示,质量分别为mA=3kg、mB=1kg的物块A、B置于足够长的水平面上,F=13N的水平推力作用下,一起由静止开始向右做匀加速运动,已知A、B与水平面间的动摩擦因素分别为μA=0.1、μB=0.2,取g=10m/s2.
如图所示,质量分别为mA=3kg、mB=1kg的物块A、B置于足够长的水平面上,F=13N的水平推力作用下,一起由静止开始向右做匀加速运动,已知A、B与水平面间的动摩擦因素分别为μA=0.1、μB=0.2,取g=10m/s2. 如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在大小相等的两力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),斜向上的力F与水平方向成θ角,轻弹簧与水平方向成α角.则m1所受支持力FN、摩擦力f和弹簧弹力T正确的是( )
如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在大小相等的两力F的作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),斜向上的力F与水平方向成θ角,轻弹簧与水平方向成α角.则m1所受支持力FN、摩擦力f和弹簧弹力T正确的是( ) 如图所示,质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到稳定时,两球离轴的距离保持不变,则有( )
如图所示,质量分别为m1、m2的小球A、B可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到稳定时,两球离轴的距离保持不变,则有( ) 如图所示,质量分别为M和m的两个小球A、B套在光滑水平直杆P上,整个直杆被固定于竖直转轴上,并保持水平,两球间用劲度系数为K,自然长度为L的轻质弹簧连接在一起,左边小球被轻质细绳拴在竖直转轴上,细绳长度也为L,现欲使横杆P随竖直转轴一起在水平面内匀速转动,其角速度为ω,求当弹簧长度稳定后,细绳的拉力和弹簧的总长度各为多少?
如图所示,质量分别为M和m的两个小球A、B套在光滑水平直杆P上,整个直杆被固定于竖直转轴上,并保持水平,两球间用劲度系数为K,自然长度为L的轻质弹簧连接在一起,左边小球被轻质细绳拴在竖直转轴上,细绳长度也为L,现欲使横杆P随竖直转轴一起在水平面内匀速转动,其角速度为ω,求当弹簧长度稳定后,细绳的拉力和弹簧的总长度各为多少? 如图所示,质量分别为mA、mB的A、B两物体置于动摩擦因数为μ的粗糙水平面上,它们之间用轻质弹簧连接,在A上施加一个水平向右的恒力F,两物块一起以加速度a向右做匀加速运动,此时弹簧伸长量为x;若将力的大小增大到F'=2F时,两物块均以加速度a'做匀加速运动,此时弹簧伸长量为x',则( )
如图所示,质量分别为mA、mB的A、B两物体置于动摩擦因数为μ的粗糙水平面上,它们之间用轻质弹簧连接,在A上施加一个水平向右的恒力F,两物块一起以加速度a向右做匀加速运动,此时弹簧伸长量为x;若将力的大小增大到F'=2F时,两物块均以加速度a'做匀加速运动,此时弹簧伸长量为x',则( )