题目内容
20. 如图,质量M=4kg的木板放在光滑水平地面上,木板的长度L=9m,木板的最左端放有一质量m=2kg的物体(可视为质点)物体与木板的上表面间的动摩擦因数u=0.2,整个装置处于静止,现对物体施加一水平向右的拉力F=10N,使物体沿木板向右运动.求下面两种情况下物体经多长时间从木板的右端滑出?(g取10m/s2)
如图,质量M=4kg的木板放在光滑水平地面上,木板的长度L=9m,木板的最左端放有一质量m=2kg的物体(可视为质点)物体与木板的上表面间的动摩擦因数u=0.2,整个装置处于静止,现对物体施加一水平向右的拉力F=10N,使物体沿木板向右运动.求下面两种情况下物体经多长时间从木板的右端滑出?(g取10m/s2)(1)外力将木板固定在水平地面上不动;
(2)不加外力固定木板,将木板放置在光滑水平面上.
分析 (1)将木板固定在水平地面上不动,物体在F作用下做初速度为零的匀加速运动,由牛顿第二定律求出加速度,再由位移时间公式求时间.
(2)将木板放置在光滑水平面上,物体和木板都做匀加速运动,由牛顿第二定律分别求两者的加速度,根据位移之差等于板长,由位移时间公式求时间.
解答 解:(1)将木板固定在水平地面上不动,物体的加速度为 a1=$\frac{F-μmg}{m}$=$\frac{10-0.2×2×10}{2}$=3m/s2.
由位移时间公式得 L=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$得
t1=$\sqrt{\frac{2L}{{a}_{1}}}$=$\sqrt{\frac{2×9}{3}}$=$\sqrt{6}$s
(2)将木板放置在光滑水平面上,物体和木板都做匀加速运动,物体的加速度仍为 a1=3m/s2.
木板的加速度 a2=$\frac{μmg}{M}$=$\frac{0.2×2×10}{4}$=1m/s2.
由位移关系得:L=$\frac{1}{2}{a}_{1}{t}_{2}^{2}$-$\frac{1}{2}{a}_{2}{t}_{2}^{2}$
得 t2=$\sqrt{\frac{2L}{{a}_{1}-{a}_{2}}}$=$\sqrt{\frac{2×9}{3-1}}$s=3s
答:
(1)外力将木板固定在水平地面上不动,时间是$\sqrt{6}$s;
(2)不加外力固定木板,将木板放置在光滑水平面上,时间是3s.
点评 解决本题的关键理清物体和木板的运动情况,分析位移关系,结合牛顿第二定律和运动学公式进行研究.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
9.关于点电荷产生的电场,下列说法中正确的是( )
| A. | 当某点与点电荷距离r→0时,该点场强E→∞ | |
| B. | 当某点与点电荷间距离r→∞时,该点电场强度E→∞ | |
| C. | 没有两个点的场强是相同的 | |
| D. | 与点电荷距离相等的点处的场强是相同的 |
11. 如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.则( )
如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.则( )
 如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.则( )
如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.则( )| A. | 它们从磁场中射出时,出射点间的距离为$2\frac{mv}{eB}$ | |
| B. | 它们从磁场中射出时,出射点间的距离为$\frac{mv}{eB}$ | |
| C. | 它们从磁场中射出的时间差为$\frac{2πm}{eB}$ | |
| D. | 它们从磁场中射出的时间差为$\frac{4πm}{3eB}$ |
5.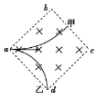 如图,两个带电量、质量均相同的带电粒子甲、乙以不同的速率从a点沿对角线ac方向射入正方形匀强磁场中,磁场方向垂直纸面向里,甲粒子垂直bc离开磁场,乙粒子从d点离开磁场,不计粒子重力,则( )
如图,两个带电量、质量均相同的带电粒子甲、乙以不同的速率从a点沿对角线ac方向射入正方形匀强磁场中,磁场方向垂直纸面向里,甲粒子垂直bc离开磁场,乙粒子从d点离开磁场,不计粒子重力,则( )
 如图,两个带电量、质量均相同的带电粒子甲、乙以不同的速率从a点沿对角线ac方向射入正方形匀强磁场中,磁场方向垂直纸面向里,甲粒子垂直bc离开磁场,乙粒子从d点离开磁场,不计粒子重力,则( )
如图,两个带电量、质量均相同的带电粒子甲、乙以不同的速率从a点沿对角线ac方向射入正方形匀强磁场中,磁场方向垂直纸面向里,甲粒子垂直bc离开磁场,乙粒子从d点离开磁场,不计粒子重力,则( )| A. | 甲粒子带正电,乙粒子带负电 | |
| B. | 甲粒子的速率是乙粒子速率的$\sqrt{2}$倍 | |
| C. | 甲粒子所受的洛伦兹力是乙粒子所受洛伦兹力的2倍 | |
| D. | 甲粒子在磁场中的运行时间是乙粒子在磁场中运动时间的一半 |
12.两相邻匀强磁场区域的磁感应强度大小不同、方向平行.一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较弱磁场区域进入到较强磁场区域后,粒子的( )
| A. | 轨道半径减小,角速度增大 | B. | 轨道半径减小,角速度减小 | ||
| C. | 轨道半径增大,角速度增大 | D. | 轨道半径增大,角速度减小 |
9.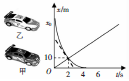 甲、乙两辆遥控玩具赛车在同一条直线上运动,通过传感器将位移信息实时传输给计算机,并绘制成x-t图象如图所示的实线,图中倾斜虚线为曲线过点(2,10)的切线,已知乙车做匀变速直线运动,其图象与t轴相切于4s处,下列判断错误的是( )
甲、乙两辆遥控玩具赛车在同一条直线上运动,通过传感器将位移信息实时传输给计算机,并绘制成x-t图象如图所示的实线,图中倾斜虚线为曲线过点(2,10)的切线,已知乙车做匀变速直线运动,其图象与t轴相切于4s处,下列判断错误的是( )
 甲、乙两辆遥控玩具赛车在同一条直线上运动,通过传感器将位移信息实时传输给计算机,并绘制成x-t图象如图所示的实线,图中倾斜虚线为曲线过点(2,10)的切线,已知乙车做匀变速直线运动,其图象与t轴相切于4s处,下列判断错误的是( )
甲、乙两辆遥控玩具赛车在同一条直线上运动,通过传感器将位移信息实时传输给计算机,并绘制成x-t图象如图所示的实线,图中倾斜虚线为曲线过点(2,10)的切线,已知乙车做匀变速直线运动,其图象与t轴相切于4s处,下列判断错误的是( )| A. | 2s时乙车速度大于甲车 | B. | 甲车的速度大小为5m/s | ||
| C. | 乙车的加速度大小为5m/s2 | D. | 乙车的初位置在x0=50m处 |
10.下列说法中正确的是( )
| A. | ${\;}_{92}^{238}U$衰变为${\;}_{86}^{222}Rn$要经过4次α衰变和2次β衰变 | |
| B. | ${\;}_{92}^{235}U$的半衰期约为7亿年,随着地球环境的不断变化,其半衰期可能会变短 | |
| C. | 发生光电效应时,若入射光频率确定,则光的强度越大,形成的饱和光电流越大 | |
| D. | 已知氢原子的基态能量E1=-13.6eV,一个处于基态的氢原子吸收了一个14eV的光子后被电离 |
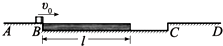 在平台AD中间有一个长为$\frac{4}{3}$l的凹槽BC,质量为m的滑板上表面与平台AD等高,质量为2m的铁块(可视为质点)与滑板间动摩擦因数为?1,铁块以一定初速度滑上滑板后,滑板开始向右做匀加速运动,当滑板右端到达凹槽右端C时,铁块与滑板速度恰好相等,滑板与凹槽右侧边碰撞后立即原速反弹,左端到达凹槽B端时速度恰好为零,而铁块则滑上平台CD.重力加速度为g.求:
在平台AD中间有一个长为$\frac{4}{3}$l的凹槽BC,质量为m的滑板上表面与平台AD等高,质量为2m的铁块(可视为质点)与滑板间动摩擦因数为?1,铁块以一定初速度滑上滑板后,滑板开始向右做匀加速运动,当滑板右端到达凹槽右端C时,铁块与滑板速度恰好相等,滑板与凹槽右侧边碰撞后立即原速反弹,左端到达凹槽B端时速度恰好为零,而铁块则滑上平台CD.重力加速度为g.求: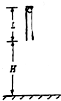 如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.管从下端离地面距离为H=5m处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,由于管落地时与地面作用时间很短,在管碰地时间内可认为球的速度不变.不计空气阻力,重力加速度为g=10m/s2.求:
如图所示,一个质量为M长为L的圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg.管从下端离地面距离为H=5m处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,由于管落地时与地面作用时间很短,在管碰地时间内可认为球的速度不变.不计空气阻力,重力加速度为g=10m/s2.求: