题目内容
8．
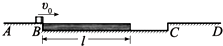在平台AD中间有一个长为$\frac{4}{3}$l的凹槽BC，质量为m的滑板上表面与平台AD等高，质量为2m的铁块（可视为质点）与滑板间动摩擦因数为?1，铁块以一定初速度滑上滑板后，滑板开始向右做匀加速运动，当滑板右端到达凹槽右端C时，铁块与滑板速度恰好相等，滑板与凹槽右侧边碰撞后立即原速反弹，左端到达凹槽B端时速度恰好为零，而铁块则滑上平台CD．重力加速度为g．求：（1）若滑板反弹后恰好能回到凹槽左端，则滑板与凹槽间动摩擦因数?2多大？
（2）铁块滑上滑板时的初速度v0．
分析 （1）把滑板作为研究对象，题设有两个过程：①从铁块滑上开始的到与恰恰与C点相撞，这是一个匀加速直线运动过程．②从反弹开始到B端速度恰好为零，这是一个匀减速直线运动过程，分别应用牛顿第二定律和运动学公式，联立可求得滑板与凹槽间动摩擦因数?2．
（2）对铁块来说，只有一个匀减速直线运动过程，从滑上滑板开始到刚到达C点，其速度减为零，同理，先用牛顿第二定律求其加速度，然后用运动学公式求初速度．
解答 解：（1）设滑板向右加速滑动时加速度大小为a1，反弹左滑时加速度大小为a2，
滑板与凹槽右端碰撞时的速度为v，由运动规律得滑板向右做初速度为零的匀加速运动：
${v}^{2}=2{a}_{1}×\frac{1}{3}l$ ①
反弹后向左做匀减速运动，末速度为零$0-{v}^{2}=2（-{a}_{2}）×\frac{1}{3}l$ ②
滑板向右运动时水平方向受到铁块向右的滑动摩擦力和槽底向左的滑动摩擦力，向左滑动时
只受槽底向右的滑动摩擦力，由牛顿第二定律得
μ12mg-μ23mg=ma1 ③
μ2mg=ma2 ④
联立①②③④解得 ${μ_2}=\frac{1}{2}{μ_1}$ ⑤
（2）由②④⑤式得 $v=\frac{\sqrt{3{μ}_{1}gl}}{3}$ ⑥
铁块向右滑动的加速度大小为a，则μ12mg=2ma ⑦
铁块向右做匀减速运动，有${v}^{2}-{{v}_{0}}^{2}=2（-a）×\frac{4}{3}l$ ⑧
由⑥⑦⑧解得 v0=$\sqrt{3{μ}_{1}gl}$ ⑨
答：（1）若滑板反弹后恰好能回到凹槽左端，则滑板与凹槽间动摩擦因数?2为$\frac{1}{2}{μ}_{1}$．
（2）铁块滑上滑板时的初速度v0为$\sqrt{3{μ}_{1}gl}$．
点评 本题的难点在于连接体问题：由于相互作用的两个物体运动状态不同，只能用隔离法来求解，只有先对物体的受力分析准确无误，才能相关规律求出加速度，最后再求力和运动学量，这其中当然涉及到的是牛顿第二定律和运动学规律．
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{24}$ |
一含有理想变压器的电路如图所示，变压器原副线圈匝数比n1：n2=2，图中电阻R1、R2和R3的阻值分别是4Ω、2Ω和3Ω，U为有效值恒定的正弦交流电压源．当开关S断开时，理想电流表的示数为I．当S闭合时，电流表的示数为（ ）| A． | $\frac{2}{3}$I | B． | $\frac{1}{2}$I | C． | $\frac{3}{2}$I | D． | 2I |
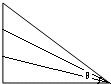如图所示，一物体从底边相等（均为l）的各种长度不等的光滑斜面顶端由静止滑下，则当斜面倾角θ=45°时，物体滑到斜面底部所用时间最短，最短时间tmin=2$\sqrt{\frac{l}{g}}$． 
质量为m=2kg的物体，位于粗糙水平面上，在大小为F=5N、方向与水平成α=37°的斜向下的推力作用下，从静止起运动t1=2s，通过s1=2m，第2s末撤去F．试求：
如图所示，水平地面上，光滑物块甲从A点在外力作用下以a1=4m/s2的加速度由静止开始向右运动，同时物块乙从B点以初速度v0水平向左运动．从甲、乙开始运动计时，经时间t=1.0s两物块相遇．已知物块乙与水平面间的动摩擦因数μ=0.2，A、B两点间的距离s=4m．取重力加速度g=10m/s2，求：
如图，质量M=4kg的木板放在光滑水平地面上，木板的长度L=9m，木板的最左端放有一质量m=2kg的物体（可视为质点）物体与木板的上表面间的动摩擦因数u=0.2，整个装置处于静止，现对物体施加一水平向右的拉力F=10N，使物体沿木板向右运动．求下面两种情况下物体经多长时间从木板的右端滑出？（g取10m/s2）| A． | 布朗运动是液体分子的运动，说明液体分子在永不停息地做无规则热运动 | |
| B． | 足球充足气后很难压缩，是因为足球内气体分子间斥力作用的结果 | |
| C． | 自然界中只要涉及热现象的宏观过程都具有方向性 | |
| D． | 一定质量的理想气体，如果压强不变，体积增大，那么它一定从外界吸热 |