题目内容
11. 如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.则( )
如图所示,直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从O点以与MN成30°角的相同速度v射入该磁场区域(电子质量为m,电量为e),经一段时间后从边界MN射出.则( )| A. | 它们从磁场中射出时,出射点间的距离为$2\frac{mv}{eB}$ | |
| B. | 它们从磁场中射出时,出射点间的距离为$\frac{mv}{eB}$ | |
| C. | 它们从磁场中射出的时间差为$\frac{2πm}{eB}$ | |
| D. | 它们从磁场中射出的时间差为$\frac{4πm}{3eB}$ |
分析 粒子做匀速圆周运动,由洛仑兹力充当向心力可知两粒子离开磁场时的距离,则可求出出射点的距离;根据两粒子在磁场中转动的时间可知时间差.
解答 解:AB、正、负电子在匀强磁场中圆周运动半径相同但绕行方向不同,分别作出正、负电子在磁场中运动的轨迹如图所示.
由Bev=$\frac{m{v}^{2}}{R}$得:R=$\frac{mv}{Be}$
射出点距离为:PQ=4Rsinθ
T=$\frac{2πm}{eB}$
所以:θ=30°
如图可知,两粒子离开时距O点均为R,
所以出射点相距为:L=2R=$\frac{2mv}{Be}$,故A正确,B错误;
CD、由T=$\frac{2πr}{v}$得:T=$\frac{2πm}{Be}$
负电子在磁场中运动时间为:t1=$\frac{2π-2θ}{2π}$T=$\frac{5}{6}$T
正电子在磁场中运动时间为:t2=$\frac{2θ}{2π}$T=$\frac{1}{6}$T
所以两个电子射出的时间差为:△t=t1-t2=$\frac{2}{3}T$=$\frac{4πm}{3Be}$;故C错误,D正确.
故选:AD.
点评 带电粒子在电场中的运动关键在于由几何关系找出圆心和半径,再由洛仑兹力充当向心力及圆的性质可得出几何关系及转动时间.

练习册系列答案
相关题目
20.14C发生放射性衰变成为14N,半衰期约5700年.已知植物存活期间,其体内14C与12C的比例不变;生命活动结束后,14C的比例持续减小.现通过测量得知,某古木样品14C的比例正好是现代植物所制样品的二分之一.下列说法正确的是( )
| A. | 14C衰变为14N的过程中放出β射线是来自核外电子的电离 | |
| B. | 12C、13C、14C具有相同的中子数 | |
| C. | 该古木的年代距今约5700年 | |
| D. | 增加样品测量环境的压强将加速14C的衰变 |
1.下列说法中指时间间隔的是( )
| A. | 天津开往德州的 625 次列车于13时35分从天津出发 | |
| B. | 某人用15s 跑完100 m | |
| C. | 中央电视台新闻联播节目每天19 时开始 | |
| D. | 某场足球赛在开赛80分钟时,甲队才攻入一球 |
18. 一含有理想变压器的电路如图所示,变压器原副线圈匝数比n1:n2=2,图中电阻R1、R2和R3的阻值分别是4Ω、2Ω和3Ω,U为有效值恒定的正弦交流电压源.当开关S断开时,理想电流表的示数为I.当S闭合时,电流表的示数为( )
一含有理想变压器的电路如图所示,变压器原副线圈匝数比n1:n2=2,图中电阻R1、R2和R3的阻值分别是4Ω、2Ω和3Ω,U为有效值恒定的正弦交流电压源.当开关S断开时,理想电流表的示数为I.当S闭合时,电流表的示数为( )
 一含有理想变压器的电路如图所示,变压器原副线圈匝数比n1:n2=2,图中电阻R1、R2和R3的阻值分别是4Ω、2Ω和3Ω,U为有效值恒定的正弦交流电压源.当开关S断开时,理想电流表的示数为I.当S闭合时,电流表的示数为( )
一含有理想变压器的电路如图所示,变压器原副线圈匝数比n1:n2=2,图中电阻R1、R2和R3的阻值分别是4Ω、2Ω和3Ω,U为有效值恒定的正弦交流电压源.当开关S断开时,理想电流表的示数为I.当S闭合时,电流表的示数为( )| A. | $\frac{2}{3}$I | B. | $\frac{1}{2}$I | C. | $\frac{3}{2}$I | D. | 2I |
6. 电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
 电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )| A. | N=N′>G | B. | N>N′>G | ||
| C. | 木块处于超重状态 | D. | 木块处于失重状态 |
16.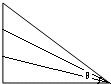 如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
 如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
如图所示,一物体从底边相等(均为l)的各种长度不等的光滑斜面顶端由静止滑下,则当斜面倾角θ=45°时,物体滑到斜面底部所用时间最短,最短时间tmin=2$\sqrt{\frac{l}{g}}$.
1.已知氢原子的基态能量为E1,激发态能量为En=$\frac{{E}_{1}}{{n}^{2}}$,其中n=2,3,4….1885年,巴尔末对当时已知的在可见光区的四条谱线做了分析,发现这些谱线的波长能够用一个公式表示,这个公式写做$\frac{1}{λ}=R({\frac{1}{2^2}-\frac{1}{n^2}})$,n=3,4,5,….式中R叫做里德伯常量,这个公式称为巴尔末公式.用h表示普朗克常量,c表示真空中的光速,则里德伯常量R可以表示为( )
| A. | $-\frac{E_1}{hc}$ | B. | $\frac{E_1}{2hc}$ | C. | $-\frac{E_1}{2hc}$ | D. | $\frac{E_1}{hc}$ |
 质量为m=2kg的物体,位于粗糙水平面上,在大小为F=5N、方向与水平成α=37°的斜向下的推力作用下,从静止起运动t1=2s,通过s1=2m,第2s末撤去F.试求:
质量为m=2kg的物体,位于粗糙水平面上,在大小为F=5N、方向与水平成α=37°的斜向下的推力作用下,从静止起运动t1=2s,通过s1=2m,第2s末撤去F.试求: 如图,质量M=4kg的木板放在光滑水平地面上,木板的长度L=9m,木板的最左端放有一质量m=2kg的物体(可视为质点)物体与木板的上表面间的动摩擦因数u=0.2,整个装置处于静止,现对物体施加一水平向右的拉力F=10N,使物体沿木板向右运动.求下面两种情况下物体经多长时间从木板的右端滑出?(g取10m/s2)
如图,质量M=4kg的木板放在光滑水平地面上,木板的长度L=9m,木板的最左端放有一质量m=2kg的物体(可视为质点)物体与木板的上表面间的动摩擦因数u=0.2,整个装置处于静止,现对物体施加一水平向右的拉力F=10N,使物体沿木板向右运动.求下面两种情况下物体经多长时间从木板的右端滑出?(g取10m/s2)