题目内容
11.为测量木块与木板间的动摩擦因数,将木反倾斜,木块以不同的初速度沿木板向上滑到最高点后再返回,用光电门测量木块来回的速度,用刻度尺测量向上运动的最大距离,为确定木块向上运动的最大高度,让木块推动轻质卡到最高点,记录这个位置,实验装置如图甲所示.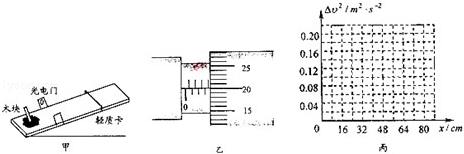
(1)本实验中,下列操作合理的是AC
A.遮光条的宽度应尽量小些
B.实验前将轻质卡置于光电门附近
C.为了实验成功,木块的倾角必须大于某一值
D.光电门与轻质卡最终位置间的距离即为木块向上运动的最大距离
(2)用螺旋测微器测量遮光条的宽度,如图乙所示读数为3.700mm.
(3)改变木块的初速度,测量出它向上运动的最大距离与木块来回经过光电门时速度的平方差,结果如下表所示,试在丙图坐标纸上作出△v2-x的图象,经测量木板倾角的余弦值为0.6,重力加速度取g=9.80m/s2,则木块与木板间的动摩擦因数为0.010(结果保留两位有效数字).
| 序号 | l | 2 | 3 | 4 | 5 |
| X/cm | 16.0 | 36.0 | 50.0 | 70.0 | 38.0 |
| △v2/m2s-2 | 0.04 | 0.09 | 0.15 | 0.19 | 0.22 |
分析 (1)根据实验步骤与实验原理分析答题;
(2)螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器示数;
(3)应用描点法作出图象;由牛顿第二定律与运动学公式求出图象函数表达式,然后根据图象与函数表达式求出动摩擦因数;
(4)根据图示实验装置与实验步骤分析实验误差
解答 解:(1)A、遮光条宽度与时间的比值是木块的平均速度,可以认为是木块通过光电门时的瞬时速度,遮光条宽度越小,平均速度越接近瞬时速度,实验误差越小,因此遮光条的宽度应尽量小些,故A正确;
B、实验时轻质卡应与木块一起向上运动,实验前将轻质卡与木块靠在一起,故B错误;
C、当木板倾角大于某一值时,木块重力沿斜面向下的分力大于最大静摩擦力,木块到达最高点后可以反向下滑,否则木块到达最高点后将静止,实验不能成功,为了实验成功,木块的倾角必须大于某一值,故C正确;
D、木块出发点与轻质卡最终位置间的距离即为木块向上运动的最大距离,故D错误;故选AC.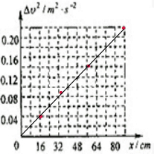 (2)由图乙所示螺旋测微器可知,螺旋测微器示数为:3.5mm+20.0×0.01mm=3.700mm.
(2)由图乙所示螺旋测微器可知,螺旋测微器示数为:3.5mm+20.0×0.01mm=3.700mm.
(3)根据表中实验数据在坐标系内描出对应点,然后根据描出的点作出图象如图所示:
由牛顿第二定律得:
木块上滑时:mgsinθ+μmgcosθ=ma1,
木块下滑时:mgsinθ-μmgcosθ=ma2,
由匀变速直线运动的速度位移公式得:
0-v02=-2a1x,v2=2a2x,
△v2=v02-v2=4μgxcosθ,
由图示图象可知,动摩擦因数:
斜率:k=4μgcosθ=$\frac{△{v}^{2}}{x}=\frac{0.20}{0.80}$=0.25,
动摩擦因数:μ=$\frac{k}{4gcosθ}=\frac{0.25}{4×9.8×0.6}$=0.010;
(4)由于轻质卡与木板间存在摩擦力,所测摩擦力实际是木块与轻质卡受到的摩擦力的合力,由于轻质卡所受摩擦力影响,所测动摩擦因数偏大.
故答案为:(1)AC;(2)3.700;(3)图象如图所示,0.010;(4)偏大
点评 本题考查了测动摩擦因数实验,知道实验原理与实验步骤是正确解题的关键;应用牛顿第二定律与匀变速运动的速度位移公式求出图象的函数表达式是正确求出动摩擦因数的前提与关键

| A. | 它始终处于静止平衡状态 | |
| B. | 运行速度大于第一宇宙速度 | |
| C. | 向心加速度与静止在赤道上物体的向心加速度大小相等 | |
| D. | “天链一号01星”与地球自转角速度相同 |
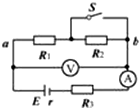 如图所示,电路中电源电动势E恒定,内阻r=2Ω,定值电阻R3=4Ω.ab段电路消耗的电功率在开关S断开与闭合时相等,电压表和电流表均为理想电表,则以下说法中正确的( )
如图所示,电路中电源电动势E恒定,内阻r=2Ω,定值电阻R3=4Ω.ab段电路消耗的电功率在开关S断开与闭合时相等,电压表和电流表均为理想电表,则以下说法中正确的( )| A. | 开关S断开时电压表的示数一定等于S闭合时的示数 | |
| B. | 电阻R1、R2可能分别为4Ω、6Ω | |
| C. | 电阻R1、R2可能分别为3Ω、9Ω | |
| D. | 开关S断开与闭合时,电压表的示数变化量与电流表的示数变化量大小之比与R1、R2无关 |
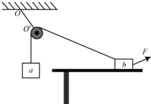 如图所示,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图所示,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )| A. | 物块b所受到的支持力也在一定范围内变化 | |
| B. | 绳OO'的张力也在一定范围内变化 | |
| C. | 连接a和b的绳的张力也在一定范围内变化 | |
| D. | 物块b与桌面间的摩擦力也在一定范围内变化 |
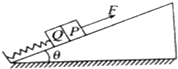 如图所示,倾角为θ的光滑足够长斜面固定在水平地面上,平行于斜面的轻弹簧一端固定在斜面底端,另一端与质量为m的物块Q连接,质量也为m的物块P挨着Q放在斜面上,初始时两物块均静止,现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,重力加速度为g,下列说法正确的是( )
如图所示,倾角为θ的光滑足够长斜面固定在水平地面上,平行于斜面的轻弹簧一端固定在斜面底端,另一端与质量为m的物块Q连接,质量也为m的物块P挨着Q放在斜面上,初始时两物块均静止,现用平行于斜面向上的力F拉物块P,使P做加速度为a的匀加速运动,重力加速度为g,下列说法正确的是( )| A. | 拉力F施加的瞬间,P、Q间的弹力大小为m(gsinθ-a) | |
| B. | 当弹簧恢复到原长时,物块Q达到速度最大值 | |
| C. | 从施加力F开始到弹簧第一次恢复到原长的过程中,力F做的功小于两物块机械能的增加量 | |
| D. | 拉力F一直增大 |
 在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )
在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )| A. | 48w | B. | 47w | C. | 32w | D. | 44w |
 用如图所示的方法可以研究不同人的反应时间,设直尺从静止开始自由下落到直尺被受测者抓住,直尺下落的竖直距离为h,受测者的反应时间为t,则下列关于t和h的关系正确的是( )
用如图所示的方法可以研究不同人的反应时间,设直尺从静止开始自由下落到直尺被受测者抓住,直尺下落的竖直距离为h,受测者的反应时间为t,则下列关于t和h的关系正确的是( )| A. | t∝h | B. | t∝$\frac{1}{h}$ | C. | t∝h2 | D. | t∝$\sqrt{h}$ |
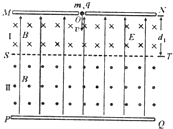 如图所示,两块很大的平行带电导体板MN、PQ产生竖直向上的匀强电场,在两导体板之间存在有理想边界的匀强磁场,匀强磁场分为I、Ⅱ两个区域,磁感应强度大小均为B,方向如图所示,ST为两磁场的边界,I区域高度为d1,Ⅱ区域的高度足够大.一个质量为m、电量为q的带正电的小球从MN板上的小孔O以一定的速度垂直射入复合场,小球恰能做匀速圆周运动并恰能回到O孔,带电小球在运动中不会与板相碰,不考虑磁场和电场之间的相互影响,重力加速度为g,求:
如图所示,两块很大的平行带电导体板MN、PQ产生竖直向上的匀强电场,在两导体板之间存在有理想边界的匀强磁场,匀强磁场分为I、Ⅱ两个区域,磁感应强度大小均为B,方向如图所示,ST为两磁场的边界,I区域高度为d1,Ⅱ区域的高度足够大.一个质量为m、电量为q的带正电的小球从MN板上的小孔O以一定的速度垂直射入复合场,小球恰能做匀速圆周运动并恰能回到O孔,带电小球在运动中不会与板相碰,不考虑磁场和电场之间的相互影响,重力加速度为g,求: