题目内容
2.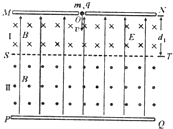 如图所示,两块很大的平行带电导体板MN、PQ产生竖直向上的匀强电场,在两导体板之间存在有理想边界的匀强磁场,匀强磁场分为I、Ⅱ两个区域,磁感应强度大小均为B,方向如图所示,ST为两磁场的边界,I区域高度为d1,Ⅱ区域的高度足够大.一个质量为m、电量为q的带正电的小球从MN板上的小孔O以一定的速度垂直射入复合场,小球恰能做匀速圆周运动并恰能回到O孔,带电小球在运动中不会与板相碰,不考虑磁场和电场之间的相互影响,重力加速度为g,求:
如图所示,两块很大的平行带电导体板MN、PQ产生竖直向上的匀强电场,在两导体板之间存在有理想边界的匀强磁场,匀强磁场分为I、Ⅱ两个区域,磁感应强度大小均为B,方向如图所示,ST为两磁场的边界,I区域高度为d1,Ⅱ区域的高度足够大.一个质量为m、电量为q的带正电的小球从MN板上的小孔O以一定的速度垂直射入复合场,小球恰能做匀速圆周运动并恰能回到O孔,带电小球在运动中不会与板相碰,不考虑磁场和电场之间的相互影响,重力加速度为g,求:(1)匀强电场的电场强度E;
(2)小球的速度大小及在复合场中运动的时间.
分析 (1)根据小球所受电场力的方向与场强方向的关系判断小球电性,根据电场力与重力的关系求出电场强度大小.
(2)小球在磁场中做匀速圆周运动,作出小球的运动轨迹,由几何知识求出轨道半径,应用牛顿第二定律分析答题.
解答 解:(1)小球进入电磁场后恰好能做匀速圆周运动,则重力与电场力合力为零,洛伦兹力提供向心力,
重力竖直向下,则电场力竖直向上,电场强度向上,电场力方向与场强方向相同,则小球带正电;
电场力与重力相等,则有:qE=mg…①,
则电场强度:E=$\frac{mg}{q}$…②
(2)小球在磁场中做匀速圆周运动,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{R}$…③
由于小球在Ⅰ、Ⅱ两个区域运动过程中q、v、B、m的大小不变,则三段圆弧的半径相等,
以三个圆心为顶点的三角形为等边三角形,边长为2R,内角为60度,如图所示,
由几何知识可得:R=$\frac{{d}_{1}}{sin60°}$…④,
所以:v=$\frac{2\sqrt{3}Bq{d}_{1}}{3m}$
粒子在磁场中运动周期:T=$\frac{2πR}{v}$…⑤
小球运动过程中转过的角度:θ总=$\frac{π}{3}+\frac{5π}{3}+\frac{π}{3}=\frac{7π}{3}$…⑥;
又:$\frac{t}{T}=\frac{{θ}_{总}}{2π}$…⑦
联立得:t=$\frac{7πm}{3qB}$
答:(1)匀强电场的电场强度是$\frac{mg}{q}$;
(2)小球的速度大小是$\frac{2\sqrt{3}Bq{d}_{1}}{3m}$,在复合场中运动的时间是$\frac{7πm}{3qB}$.
点评 本题考查了带电小球在磁场中的运动,分析清楚小球的运动过程,作出小球的运动轨迹、应用牛顿第二定律等公式即可正确解题;分析清楚运动过程、作出小球运动轨迹是正确解题的关键.

 智能训练练测考系列答案
智能训练练测考系列答案 如图所示,为正电荷Q的电场,A、B是电场中的两点,将电量为q=5×10-8库仑的正点电荷(试探电荷)置于A点,所受电场力为2×10-3牛,则下列判断正确的是( )
如图所示,为正电荷Q的电场,A、B是电场中的两点,将电量为q=5×10-8库仑的正点电荷(试探电荷)置于A点,所受电场力为2×10-3牛,则下列判断正确的是( )| A. | 将点电荷q从A点移走,则该点的电场强度为零 | |
| B. | 将电量为q的负点电荷放于A点,A点场强大小为4.0×104N/C,方向指向B | |
| C. | B点处的电场强度小于4.0×104N/C | |
| D. | 将电量为2q的正点电荷放于A点,A点场强大小为8.0×104 N/C,方向指向B |
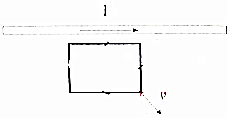 如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )
如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )| A. | 金属框中无电流,一直做匀速直线运动 | |
| B. | 金属框最终在水平面上做匀速直线运动 | |
| C. | 金属框最终将静止在水平面上的某处 | |
| D. | 金属框中产生的热量最多为0.04J |
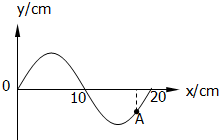 如图,为一列沿x轴正方向传播的简谐波在某时刻的波形图,A是参与波动的介质中的一个质点,若波源的振动周期为T=1s,则从该时刻起质点运动到平衡位置所需的时间可能为( )
如图,为一列沿x轴正方向传播的简谐波在某时刻的波形图,A是参与波动的介质中的一个质点,若波源的振动周期为T=1s,则从该时刻起质点运动到平衡位置所需的时间可能为( )| A. | 0.1s | B. | 0.2s | C. | 0.3s | D. | 0.5s |
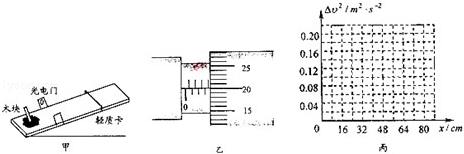
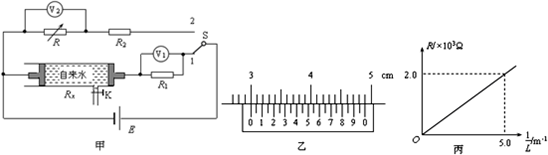
(1)本实验中,下列操作合理的是AC
A.遮光条的宽度应尽量小些
B.实验前将轻质卡置于光电门附近
C.为了实验成功,木块的倾角必须大于某一值
D.光电门与轻质卡最终位置间的距离即为木块向上运动的最大距离
(2)用螺旋测微器测量遮光条的宽度,如图乙所示读数为3.700mm.
(3)改变木块的初速度,测量出它向上运动的最大距离与木块来回经过光电门时速度的平方差,结果如下表所示,试在丙图坐标纸上作出△v2-x的图象,经测量木板倾角的余弦值为0.6,重力加速度取g=9.80m/s2,则木块与木板间的动摩擦因数为0.010(结果保留两位有效数字).
| 序号 | l | 2 | 3 | 4 | 5 |
| X/cm | 16.0 | 36.0 | 50.0 | 70.0 | 38.0 |
| △v2/m2s-2 | 0.04 | 0.09 | 0.15 | 0.19 | 0.22 |
| A. | $\frac{{R}_{1}+{R}_{2}}{2}$ | B. | $\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$ | C. | $\frac{{R}_{1}+{R}_{2}}{{R}_{1}{R}_{2}}$ | D. | $\sqrt{{R}_{1}{R}_{2}}$ |
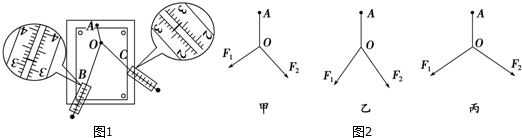
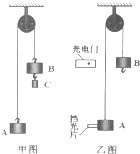 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.