题目内容
2.为了迎接太空时代的到来,美国国会通过了一项计划,在2050年前建造太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住升降机,放开绳,升降机能到达地球上,人坐在升降机里,在卫星上通过电动机把升降机拉到卫星上.已知地球表面的重力加速度g=10m/s2,地球半径R=6400km.求:(1)某人在地球表面用弹簧测力计称得重800N,站在升降机中.当升降机以加速度a=g(g为地球表面处的重力加速度)垂直地面上升,这时此人再一次用同一弹簧测力计称得视重为880N,忽略地球公转的影响,求升降机此时距地面的高度;
(2)如果把绳的一端搁置在同步卫星上,绳的长度至少为多少米?(保留两位有效数字)
分析 根据牛顿第二定律求出当时的重力加速度,根据万有引力等于重力,得出轨道半径,从而得出高度.
通过万有引力提供向心力,求出同步卫星的轨道半径,从而知道绳的长度.
解答 解:(1)由题意可知人的质量为:m=80kg
对人根据牛顿第二定律得:880-mg′=mg
根据万有引力等于重力得:
mg′=$\frac{GMm}{{(R+h)}^{2}}$,
$\frac{GMm}{{R}^{2}}$=mg
解得:g′=${(\frac{R}{R+h})}^{2}$g
即h=2.16R=1.38×107m
(2)同步卫星围绕行星做匀速圆周运动,由地球对卫星的万有引力提供卫星所需的向心力列出等式:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$,
r=R+h′
T为地球自转周期,结合GM=gR2.
得:h′=3.6×107m
答:(1)升降机此时距地面的高度是1.38×107m;
(2)如果把绳的一端搁置在同步卫星上,绳的长度至少为3.6×107m
点评 卫星所受的万有引力等于向心力、万有引力等于重力是卫星类问题必须要考虑的问题,本题根据这两个关系即可列式求解!

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12. 如图所示,将粗糙的斜面体放在粗糙水平地面上,物块m放在斜面上,恰能沿斜面匀速下滑,斜面体静止不动.若用平行斜面向下的推力,使物块加速下滑,则斜面体( )
如图所示,将粗糙的斜面体放在粗糙水平地面上,物块m放在斜面上,恰能沿斜面匀速下滑,斜面体静止不动.若用平行斜面向下的推力,使物块加速下滑,则斜面体( )
 如图所示,将粗糙的斜面体放在粗糙水平地面上,物块m放在斜面上,恰能沿斜面匀速下滑,斜面体静止不动.若用平行斜面向下的推力,使物块加速下滑,则斜面体( )
如图所示,将粗糙的斜面体放在粗糙水平地面上,物块m放在斜面上,恰能沿斜面匀速下滑,斜面体静止不动.若用平行斜面向下的推力,使物块加速下滑,则斜面体( )| A. | 受到地面的摩擦力大小为零 | B. | 受到地面的摩擦力方向水平向右 | ||
| C. | 对地面的压力变大 | D. | 可能沿水平面向右运动 |
10. 如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )
如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )
 如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )
如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )| A. | 在同种介质中b光的速度较大 | |
| B. | 该玻璃三棱镜对a 光的折射率较小 | |
| C. | 若让a、b光分别照射同种金属,都能发生光电效应,则b光照射金属产生光电子的最大初动能较大 | |
| D. | 若让a、b光分别通过同一双缝装置,在同位置的屏上形成干涉图样,则b光条纹间距较大 |
7. 如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )
如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )
 如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )
如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )| A. | 当t=$\frac{L}{v}$时,水平拉力有最大值为$\frac{{B}^{2}{L}^{2}v}{R}$ | |
| B. | 当t=$\frac{2L}{v}$时,水平拉力有最大功率为$\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$ | |
| C. | 在0~$\frac{L}{v}$时间内,水平拉力做功为$\frac{{B}^{2}{L}^{3}v}{2R}$ | |
| D. | 在0~$\frac{L}{v}$和$\frac{L}{v}$~$\frac{2L}{v}$两段时间内水平拉力做功相同 |
5.做离心运动的物体,下面说法正确的是( )
| A. | 离心现象是因为向心力小于离心力 | |
| B. | 离心现象是因为合外力不足以提供物体做圆周运动所需向心力 | |
| C. | 速度的大小改变,方向不变 | |
| D. | 速度大小和方向都可能改变 |
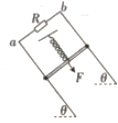 如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,导轨电阻不计,上端a,b间接有阻值为R的定值电阻,匀强磁场垂直于导轨平面,磁感应强度的大小为B.质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上,并处于静止状态,现对导体棒施加一个平行于导轨向下的恒力F,导体棒在经过一系列复杂的运动后,最终静止.整个运动过程中导体棒始终与导轨垂直且接触良好,已知弹簧的劲度系数为k,弹簧的重心轴线与导轨ab垂直,重力加速度为g,求:
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,导轨电阻不计,上端a,b间接有阻值为R的定值电阻,匀强磁场垂直于导轨平面,磁感应强度的大小为B.质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上,并处于静止状态,现对导体棒施加一个平行于导轨向下的恒力F,导体棒在经过一系列复杂的运动后,最终静止.整个运动过程中导体棒始终与导轨垂直且接触良好,已知弹簧的劲度系数为k,弹簧的重心轴线与导轨ab垂直,重力加速度为g,求: 在光滑的水平面上有两个小球A和B,如图,他们的质量分别是mA=2kg和mB=4kg.
在光滑的水平面上有两个小球A和B,如图,他们的质量分别是mA=2kg和mB=4kg. 如图所示,质量分别为M和m的物块与劲度系数为k的轻质弹簧两端相连,物块M放在地面上,用竖直向下的大小为F的恒力,压在物块m上,直到物块m运动至最低点时撤去恒力,此后物块m将向上运动.已知弹簧的弹性势能与形变量的关系为EP=$\frac{1}{2}$kx2.
如图所示,质量分别为M和m的物块与劲度系数为k的轻质弹簧两端相连,物块M放在地面上,用竖直向下的大小为F的恒力,压在物块m上,直到物块m运动至最低点时撤去恒力,此后物块m将向上运动.已知弹簧的弹性势能与形变量的关系为EP=$\frac{1}{2}$kx2. 某同学在进行“研究平抛物体的运动”实验:
某同学在进行“研究平抛物体的运动”实验: