��Ŀ����
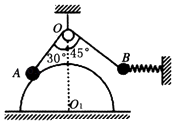
����Ŀ����ͼ������������Ϊm��Сľ��a��b������Ϊ�ʵ㣩����ˮƽԲ���ϣ�a��ת��OO��ľ���Ϊl��b��ת��ľ���Ϊ2l��ľ����Բ�̵����Ħ����Ϊľ������������k�����������ٶȴ�СΪg����Բ�̴Ӿ�ֹ��ʼ��ת�Ỻ���ؼ����˶����æر�ʾԲ��ת���Ľ��ٶȣ�����˵����ȷ���ǣ� ��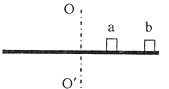
A.bһ����a�ȿ�ʼ����
B.a��b���ܵ�Ħ����ʼ�����
C.����= ![]() ʱ��b��ʼ�������ٽ���ٶ�
ʱ��b��ʼ�������ٽ���ٶ�
D.����= ![]() ʱ��a����Ħ�����Ĵ�СΪkmg
ʱ��a����Ħ�����Ĵ�СΪkmg
���𰸡�A,C
���������⣺A��B������ľ������Ħ������ȣ�ľ����Բ��һ��ת������Ħ�����ṩ����������ţ�ٵڶ����ɵã�ľ�����ܵľ�Ħ����f=m��2r��m������ȣ�f��r������b���ܵľ�Ħ��������a�ľ�Ħ��������Բ�̵Ľ��ٶ�����ʱb�ľ�Ħ�����ȴﵽ���ֵ������bһ����a�ȿ�ʼ��������A��ȷ��B����
C����b��Ҫ����ʱ����kmg=m��22l����ã���= ![]() ����C��ȷ��
����C��ȷ��
D����aΪ�о�������= ![]() ʱ����ţ�ٵڶ����ɵã�
ʱ����ţ�ٵڶ����ɵã�
f=m��2l���ɽ�ã�f= ![]() ����D����
����D����
��ѡ��AC��
�����㾫�����������⣬������Ҫ�˽�����Բ���˶�(����Բ���˶����ٶȵĴ�С�㶨�����ٶȡ����ں�Ƶ�ʶ��Ǻ㶨����ģ����ļ��ٶȺ��������Ĵ�СҲ���Ǻ㶨����ģ����ٶȴ�С������ٶȷ���ʱ���ڱ�ı��������˶�)����Ҫ����������(����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ��������)�����֪ʶ���Ǵ���Ĺؼ���

����Ŀ������ͼ1��ʾ��װ�ÿɲ���������б�����˶��ļ��ٶȣ�һб���ϰ�װ����������ţ����й�����ҹ̶���б���Ͽ����˴�������ż�λ�ÿ��ƶ�����һ�����ڹ�Ƭ�Ļ�����б���ϻ���ʱ������������Ŷ������ļ�ʱ��������ʾ���ڹ�Ƭ�ӹ���ż��������õ�ʱ��t���ı����ż�λ�ý��ж�β�����ÿ�ζ�ʹ�����ͬһ���ɾ�ֹ��ʼ�»��������׳߲����ס���֮��ľ���s��������Ӧ��tֵ���������������ʾ�����������պ���ͼ��
s��m�� | 0.500 | 0.600 | 0.700 | 0.800 | 0.900 | 0.950 |
t��s�� | 0.29 | 0.37 | 0.45 | 0.55 | 0.67 | 0.78 |
s/t��m/s�� | 1.71 | 1.62 | 1.55 | 1.45 | 1.34 | 1.22 |
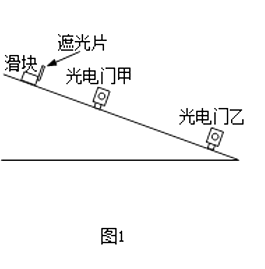
��1������������Ħ����Ϊһ������������ٶȵĴ�Сa�����龭���������ʱ��˲ʱ�ٶ�v1������ֵs��t�ĸ�������֮��������Ĺ�ϵʽ����
��2�����ݱ��и��������ݣ���ͼ2����������ֽ�ϻ��� ![]() ��tͼ�ߣ�
��tͼ�ߣ�
��3������������ ![]() ��tͼ�ߣ��ó�������ٶȵĴ�СΪa=m/s2������2λ��Ч���֣���
��tͼ�ߣ��ó�������ٶȵĴ�СΪa=m/s2������2λ��Ч���֣���