题目内容
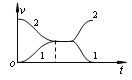
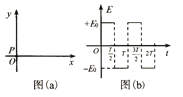
【题目】如图(a)所示的xoy平面处于匀强电场中,电场方向与x轴平行,电场强度E随时间t变化的周期为T,变化图线如图(b)所示,E为+E0时电场强度的方向沿x轴正方向.有一带正电的粒子P,在某一时刻t0以某一速度v沿Y轴正方向自坐标原点O射入电场,粒子P经过时间T到达的点记为A(A点在图中未画出).若t0=0,则OA连线与Y轴正方向夹角为45°,不计粒子重力:
(1)求粒子的比荷;
(2)若![]() ,求A点的坐标;
,求A点的坐标;
(3)若![]() ,求粒子到达A点时的速度.
,求粒子到达A点时的速度.
【答案】(1)![]() (2)(0,vT)(3)v
(2)(0,vT)(3)v
【解析】(1)粒子在t0=0时刻射入电场,粒子沿y轴方向匀速运动,位移大小为![]()
粒子沿x轴方向在![]() 内做初速度为零的匀加速运动,位移为x1,末速度为v1,则:
内做初速度为零的匀加速运动,位移为x1,末速度为v1,则:![]()
粒子沿x轴方向在![]() 内做匀减速运动,位移为x2,则:
内做匀减速运动,位移为x2,则:![]()
粒子沿x轴方向的总位移为x,则:![]()
粒子只受到电场力作用,由牛顿第二定律得:![]()
由题意OA与y轴正方向夹角为45°,则:![]() ,解得:
,解得:![]()

(2)粒子在![]() 时刻射入电场,粒子沿y轴方向匀速运动,位移大小为:
时刻射入电场,粒子沿y轴方向匀速运动,位移大小为:![]()
粒子沿x轴方向在![]() 内做初速度为零的匀加速运动,位移为x3,末速度为v2,则:
内做初速度为零的匀加速运动,位移为x3,末速度为v2,则:![]()
粒子沿x轴方向在![]() 内做匀变速运动,位移为x4,末速度为v3,则:
内做匀变速运动,位移为x4,末速度为v3,则:![]() ,
,![]()
粒子沿x轴方向在![]() 内做匀变速运动,位移为x5,则:
内做匀变速运动,位移为x5,则:![]()
粒子沿x轴的总位移为x′,则:![]() 解得:x’=0
解得:x’=0
则A点的坐标为(0,vT)
(3)粒子在![]() 时刻射入电场,粒子沿y轴方向匀速运动,速度不变;沿x轴方向在
时刻射入电场,粒子沿y轴方向匀速运动,速度不变;沿x轴方向在![]() 内做初速度为零的匀加速运动,末速度为v4,则:
内做初速度为零的匀加速运动,末速度为v4,则:![]()
粒子沿x轴方向在![]() ~T内做匀变速运动,末速度为v5,则:
~T内做匀变速运动,末速度为v5,则:![]()
粒子沿x轴方向在![]() 内做匀变速运动,末速度为
内做匀变速运动,末速度为![]() ,则
,则![]() ,解得
,解得![]() ,则:粒子通过A点的速度为v.
,则:粒子通过A点的速度为v.

【题目】利用打点计时器研究一个约1.4m高的商店卷帘窗的运动.将纸带粘在卷帘底部,纸带通过打点计时器随帘在竖直面内向上运动.打印后的纸带如下图所示,数据如表格所示.纸带中AB、BC、CD……每两点之间的时间间隔为0.10s,根据各间距的长度,可计算出卷帘窗在各间距内的平均速度v平均.可以将v平均近似地作为该间距中间时刻的即时速度v.
(1)请根据所提供的纸带和数据,绘出卷帘窗运动的v-t图像.
(2)AD段的加速度为______m/s2,AK段的平均速度为______m/s.
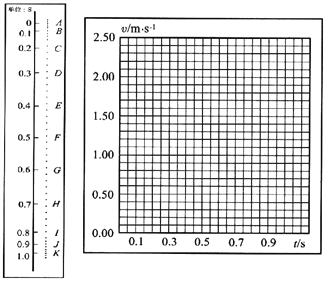
卷帘运动数据
间隔 | 间距 (cm) |
AB | 5.0 |
BC | 10.0 |
CD | 15.0 |
DE | 20.0 |
EF | 20.0 |
FG | 20.0 |
GH | 20.0 |
IH | 17.0 |
IJ | 8.0 |
JK | 4.0 |