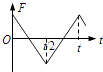��Ŀ����
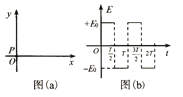
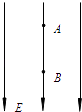
����Ŀ����ͼ��ʾ����y��0�Ŀռ��д�����ǿ�糡����ǿ��y�Ḻ������y��0�Ŀռ��У�������ǿ�ų����ų�����ֱxyƽ�棨ֽ�棩���⣮һ�����Ϊq������Ϊm�Ĵ�������˶����ӣ�����y����y=h���ĵ�P1ʱ����Ϊv0 �� ������x��������Ȼ����x����x=2h���� P2�����ų���������y����y=��2h����P3�㣮����������
��
��1���糡ǿ�ȵĴ�С��
��2�����ӵ���P2ʱ�ٶȵĴ�С�ͷ���
��3���Ÿ�Ӧǿ�ȵĴ�С��
��4�����Ӵ�P1���˶���P3������ʱ�䣮
���𰸡�
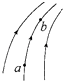
��1���⣺�����ڵ糡���ų����˶��Ĺ켣��ͼ��ʾ�������Ӵ�P1��P2��ʱ��Ϊt���糡ǿ�ȵĴ�СΪE�������ڵ糡�еļ��ٶ�Ϊa����ţ�ٵڶ����ɼ��˶�ѧ��ʽ��
qE=ma
2h=v0t
![]()
��� ![]()
�𣺵糡ǿ�ȵĴ�СΪ ![]()

��2���⣺���ӵ���P2ʱ�ٶ���x����ķ�����Ϊv0����v1��ʾ�ٶ���y��������Ĵ�С��v��ʾ�ٶȵĴ�С���ȱ�ʾ�ٶȺ�x��ļнǣ����� ![]()
![]()
��� ![]() ��
��
![]()
���ԣ���=45��
�����ӵ���P2ʱ�ٶȵĴ�СΪ ![]() ��������ˮƽ����ļн���45��
��������ˮƽ����ļн���45��
��3���⣺��ų��ĴŸ�Ӧǿ��ΪB����������������������������Բ���˶�����r��ʾԲ�ܵİ뾶����ţ�ٵڶ����� ![]()
��ΪOP2=OP3����=45�㣬�ɼ��ι�ϵ��֪������P2P3ΪԲ�����ֱ����
�ɴ˿����r= ![]()
��� ![]()
�𣺴Ÿ�Ӧǿ�ȵĴ�С ![]()
��4���⣺�����ڵ糡���˶�ʱ�� ![]()
�����ڵ糡���˶�ʱ�� ![]()
���Ӵ�P1���˶���P3������ʱ��t=t1+t2
�� ![]()
�����Ӵ�P1���˶���P3������ʱ�� ![]()
����������1�������ڵ糡����ƽ���˶�����ţ�ٵڶ����ɼ��˶�ѧ��ʽ������õ糡ǿ��E�Ĵ�С����2�����Ӵ�P��O�Ĺ����е糡�������������ö��ܶ�����ʽ��������ٶȵĴ�С����3�������ة�y�������ų�ʱ�������ֶ����жϿ�֪��������ƫת��������Բ���˶��������������䵱������������ţ�ٵڶ����ɿ������켣�뾶r������x0=2r����4���ֶ���ʱ�䣺�糡�������˶�ѧ��ʽ��ʱ�䣬�ų��������˶��˰�����ڣ�������ʱ�䣮

����Ŀ��ijͬѧ�����һ��̽�����ٶ�a���������ܺ���F������m��ϵ��ʵ�飬��ͼ����ʾΪʵ��װ�ü�ͼ��(�������Ƶ��Ϊ50 Hz)


��
��1�����ʵ��_______________�����Ҫ������Ҫ����ƽ��Ħ������
��2��ɰͰ��ɰ������m_______С��������M.
(3)ͼ����ʾΪij��ʵ��õ���ֽ��������ֽ�������С���ļ��ٶȴ�СΪ________ m/s2��
(4)����С�̼�����������������䣬�ı�С������m���ֱ�õ�С���ļ��ٶ�a��С������m����Ӧ��![]() ���������±���
���������±���
a/(m��s��2) | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
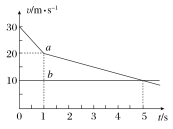
������ͼ��ʾ������ֽ�л���a ��![]() ��ͼ����ͼ�����С���ļ��ٶ�a�������ĵ���
��ͼ����ͼ�����С���ļ��ٶ�a�������ĵ���![]() ֮��Ĺ�ϵʽ��________��
֮��Ĺ�ϵʽ��________��