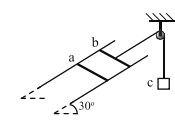
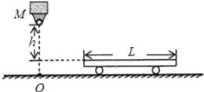
[题目]如图所示是个游乐场地.半径为的光滑四分之一圆弧轨道与长度为的水平传送带平滑连接.传送带沿顺时针方向匀速运动.速度大小为.传送带端靠近倾角为30°的足够长斜面的底端.二者间通过一小段光滑圆弧平滑连接.滑板与传送带和斜面间相对运动时的阻力分别为正压力的和.某少年踩着滑板从点沿圆弧轨道由静止滑下.到达点时立即向前跳� 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示是个游乐场地，半径为的光滑四分之一圆弧轨道与长度为的水平传送带平滑连接，传送带沿顺时针方向匀速运动，速度大小为，传送带端靠近倾角为30°的足够长斜面的底端，二者间通过一小段光滑圆弧（图中未画出）平滑连接，滑板与传送带和斜面间相对运动时的阻力分别为正压力的和。某少年踩着滑板从点沿圆弧轨道由静止滑下，到达点时立即向前跳出。该少年离开滑板后，滑板以的速度返回，少年落到前方传送带上随传送带一起匀速运动的相同滑板上，然后一起向前运动，此时滑板与点的距离为。已知少年的质量是滑板质量的9倍，不计滑板的长度以及人和滑板间的作用时间，重力加速度，求：

(1)少年跳离滑板时的速度大小；

(2)少年与滑板到达传送带最右侧端的速度大小；

(3)少年落到滑板上后至第一次到达斜面最高点所用的时间（结果保留两位小数）。

【答案】(1) ；(2)；(3)

【解析】

(1)少年与滑板从点沿圆弧下滑到点的过程中机械能守恒，设少年的质量为，滑板的质量为，则，有

少年跳离板的过程中，少年与滑板水平方向动量守恒，根据动量守恒定律有

解得少年跳离滑板时的速度大小

(2)少年跳上滑板的过程中，少年与滑板水平方向的动量守恒，设传送带速度为，则有

假设少年与滑板在传送带上可以达到与传送带相同的速度，对少年与滑板在传送带上做匀减速直线运动的过程应用牛顿第二定律有

设此过程中少年与滑板位移为，由运动学公式有

解得

由于

因此假设成立，即少年与滑板在传送带上先做匀减速运动，速度与传送带速度相同后随传送带一起匀速运动，到达传送带最右侧端的速度为

(3)设少年与滑板在传送带上做匀减速直线运动的时间为，则

设少年与滑板在传送带上做匀速直线运动的时间为，则

设少年与滑板冲上斜面后的加速度大小为，根据牛顿第二定律有

设少年与滑板在斜面上向上运动的时间为，则

设少年与滑板在传送带和斜面上运动的总时间为，则

解得

练习册系列答案

相关题目

【题目】如图，两根平行金属导轨所在的平面与水平面的夹角为30°，导轨间距为0.5 m。导体棒 a、b垂直导轨放置，用一不可伸长的细线绕过光滑的滑轮将b棒与物体c相连，滑轮与b棒之间的细线平行于导轨。整个装置处于垂直导轨平面向下的匀强磁场中，磁感应强度大小为0.2 T。物体c的质量为0. 06 kg，a、b棒的质量均为0.1kg，电阻均为0.1Ω，与导轨间的动摩擦因数均为。将a、b棒和物体c同时由静止释放，运动过程中物体c不触及滑轮，a、b棒始终与两导轨接触良好。导轨电阻不计且足够长，最大静摩擦力等于滑动摩擦力，重力加速度g取10m/s2.则（　　）

A.b棒刚要开始运动时，a棒的加速度大小为3.5 m/s2

B.b棒刚要开始运动时，a棒的速度大小为5.0 m/s

C.足够长时间后a棒的加速度大小为

D.足够长时间后a棒的速度大小为7.0 m/s

【题目】如图所示，两个可导热的气缸竖直放置，它们的底部由一细管连通（忽略细管的容积）。两气缸各有一个活塞，质量分别为m1和m2，活塞与气缸无摩擦。活塞的下方为理想气体，上方为真空。当气体处于平衡状态时，两活塞位于同一高度h.（已知m1＝2m，m2＝m）

（1）在两活塞上同时各放一质量为m的物块，求气体再次达到平衡后两活塞的高度差（假定环境温度始终保持为T0）；

（2）在达到上一问的终态后，环境温度由T0缓慢上升到1.25T0，试问在这个过程中，气体对活塞做了多少功？（假定在气体状态变化过程中，两物块均不会碰到气缸顶部）。

【题目】如图所示，右端封闭左端开口的导热良好的形玻璃管两边粗细不同，粗玻璃管半径为细玻璃管半径的3倍，两管中装入高度差为的水银，右侧封闭气体长，左侧水银面距管口。现将左管口用一与玻璃管接触良好的活塞封闭图中未画出），并将活塞缓慢推入管中，直到两管水银面等高。外界大气压强为，环境温度不变，不计活塞与管内壁的摩擦。求：

①两管水银面等高时左侧气体的压强是多少；

②整个过程活塞移动的距离是多少厘米（保留三位有效数字）。

【题目】如图所示为一列简谐横波在某时刻的波形图，是平衡位置为处的质点，是平衡位置为处的质点，若点相继出现两个波峰的时间间隔为，则下列说法正确的是（　　）

A.该波的传播速度

B.若波沿轴正方向传播，则处的质点经过即可与点位移相等

C.、两质点的振动方向总是相反

D.从图示位置计时，若点比点先到达波谷，则波的传播方向沿轴负方向

E.若波沿轴正方向传播，从图示时刻计时，再经过，、两质点的位移相同

【题目】如图所示，水平地面O点的正上方的装置M每隔相等的时间由静止释放一小球，当某小球离开M的同时，O点右侧一长为L=1.2m的平板车开始以a=6.0m/s2的恒定加速度从静止开始向左运动，该小球恰好落在平板车的左端，已知平板车上表面距离M的竖直高度为h=0.45m．忽略空气的阻力，重力加速度g取10m/s2．

（1）求小车左端离O点的水平距离；

（2）若至少有2个小球落在平板车上，则释放小球的时间间隔△t应满足什么条件？

【题目】如图所示，一桌面厚度AC=h， C到地面的高度为10h。O点为桌面上一点，O点到A的距离为2h，在O点固定一个钉子，在钉子上拴一长度为4h的轻质细线，细线另一端拴一个质量为m的小球P（可视为质点）。B在O正上方，OB距离为4h ，把小球P 拉至B点。（重力加速度为g）

(1)若小球获得一个水平向右的初速度，小球不能打在桌面上，求小球的最小初速度；

(2)给小球一水平向右的初速度，当小球恰好在竖直面内做圆周运动时，小球运动到C点正下方后瞬间细线断了。已知小球在运动过程中没有与桌腿相碰，求小球自细线断开瞬间运动到地面的水平位移和细线能承受的弹力的范围。

【题目】如图所示，在磁感应强度为、方向竖直向下的磁场中有两个固定的半径分别为和的水平放置的金属圆环形导线围成了如图回路，其总电阻为，开口很小，两开口端接有间距也为的且足够长的两个固定平行导轨，导轨与水平面夹角为，处于磁感应强度大小为、方向垂直于导轨向下的匀强磁场中。质量为、电阻为、长为的金属棒与导轨良好接触。滑动变阻器的最大电阻为，其他电阻不计，一切摩擦和空气阻力不计，重力加速度为。求：