题目内容
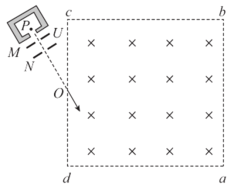
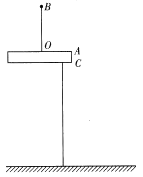
【题目】如图所示，一桌面厚度AC=h， C到地面的高度为10h。O点为桌面上一点，O点到A的距离为2h，在O点固定一个钉子，在钉子上拴一长度为4h的轻质细线，细线另一端拴一个质量为m的小球P（可视为质点）。B在O正上方，OB距离为4h ，把小球P 拉至B点。（重力加速度为g）
(1)若小球获得一个水平向右的初速度，小球不能打在桌面上，求小球的最小初速度；
(2)给小球一水平向右的初速度，当小球恰好在竖直面内做圆周运动时，小球运动到C点正下方后瞬间细线断了。已知小球在运动过程中没有与桌腿相碰，求小球自细线断开瞬间运动到地面的水平位移和细线能承受的弹力的范围。
【答案】（1）
；（2）
，
。
【解析】
(1)在小球不能打在桌面上的前提下，由分析可知，小球恰好击中
点时，小球的初速度最小，该过程小球做平抛运动，设小球
的最小初速度为
。
水平方向由
竖直方向有
解得
(2)设小球在
点的速度为
，运动到
点正下方时对应的速度设为
，在点，对小球，根据向心力公式有
从点运动到点正下方，根据动能定理有
解得
对小球，经过点正下方的前、后瞬间，细线拉力分别设为
和
，分别应用向心力公式有
解得
结合牛顿第三定律可知细线能承受的弹力范围
细线断裂后，小球做平抛运动，设小球的水平位移为
，则水平方向有
竖直方向有
联立解得
练习册系列答案
相关题目
