题目内容
10. 一半径为R的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}}{2}$R,光在真空中的传播速度为c,求:
一半径为R的$\frac{1}{4}$球体放置在水平面上,球体由折射率为$\sqrt{3}$的透明材料制成.现有一束位于过球心O的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图所示.已知入射光线与桌面的距离为$\frac{\sqrt{3}}{2}$R,光在真空中的传播速度为c,求:(i)出射角θ;
(ii)光穿越球体的时间.
分析 (i)画出光路图,作出法线,由几何知识求出光线射到球体表面的入射角,由折射定律求出折射角.由几何知识确定出光线在竖直表面上的入射角,即可由折射定律求解出射角θ.
(ii)由v=$\frac{c}{n}$求出光线在球体中的传播速度,由几何关系求出光线在球体中的传播距离,再求解时间.
解答 解:(i)设入射光线与41球体的交点为C,连接OC,OC即为入射点的法线.因此,图中的角α为入射角.过C点作球体水平表面的垂线,垂足为B,如图所示.
依题意,∠COB=α
又由△OBC知:sin α=$\frac{\sqrt{3}}{2}$
设光线在C点的折射角为β,
由折射定律得 $\frac{sinα}{sinβ}$=n
联立得 β=30°
何关系知,光线在球体的竖直表面上的入射角γ如图所示为 γ=30°
由折射定律得 $\frac{sinθ}{sinγ}$=n
解得 θ=60°.
(ii)由几何知识知△ACO为等腰三角形,故2AC•cos 30°=R
光线在球体内的传播速度为 v=$\frac{c}{n}$
设光穿越球体的时间为t,则t=$\frac{AC}{v}$
联立得 t=$\frac{R}{c}$
答:
(i)出射角θ是60°;
(ii)光穿越球体的时间是$\frac{R}{c}$.
点评 本题作光路图时,要注意当光线从球体入射时,法线就是入射点与球心的连线;当光线射出时,法线与界面垂直,本题两次使用折射定律解题.

练习册系列答案
相关题目
18. 如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )
如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )
 如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )
如图所示,桌面高度为h,质量为m的小球,从离桌面高H处自由落下,不计空气阻力,假设桌面处的重力势能为零,关于重力势能的说法正确的是( )| A. | 重力势能是矢量,有正负之分 | B. | 刚开始下落时的重力势能为mg(H+h) | ||
| C. | 落地时的重力势能为零 | D. | 落地时的重力势能为-mgh |
5. 用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )
用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )
 用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )
用如图所示实验能验证动量守恒定律.两块小木块A和B中间夹着一轻质弹簧,用细线捆在一起,放在光滑的水平台面上,将细线烧断,木块A、B被弹簧弹出,最后落在水平地面上落地点与平台边缘的水平距离分别为lA=1m,lB=2m,实验结果表明下列说法正确的是( )| A. | 木块A、B离开弹簧时的速度大小之比vA:vB=1:2 | |
| B. | 木块A、B的质量之比mA:mB=1:2 | |
| C. | 弹簧对木块A、B做功之比WA:WB=1:1 | |
| D. | 木块A、B离开弹簧时的动能之比EA:EB=1:2 |
15.甲物体的质量是乙物体质量的3倍,它们在同一高度同时自由下落,则下列说法中正确的是( )
| A. | 甲比乙先着地 | B. | 甲比乙的加速度大 | ||
| C. | 甲与乙同时着地 | D. | 甲比乙落地速度大 |
2.汽车沿平直公路做加速度大小为 0.5m/s2 的匀变速运动,那么( )
| A. | 汽车每秒钟内速度变化 0.5 m/s | |
| B. | 汽车每秒钟内加速度变化 0.5 m/s2 | |
| C. | 汽车的初速度比前 1 秒内的末速度大 0.5 m/s | |
| D. | 汽车在任意 1 s 内的末速度等于初速度的 0.5 倍 |
19. 某实验小组预测定一只小灯泡(其额定功率为0.75w,但额定电压已经模糊不清)的额定电压值,实验过程如下:
某实验小组预测定一只小灯泡(其额定功率为0.75w,但额定电压已经模糊不清)的额定电压值,实验过程如下:
他们先用多用电表的欧姆档测出小灯泡的电阻约为2Ω,然后根据公式算出小灯泡的额定电压U=$\sqrt{pR}$≈1.23v.但他们认为这样求得的额定电压值不准确,于是他们利用实验室中的器材设计了一个实验电路,进行进一步的测量.他们选择的实验器材有:
A.电压表V(量程3v,内阻约3kΩ)
B.电流表A1(量程150mA,内阻约2Ω)
C.电流表A2(量程500mA,内阻约0.6Ω)
D.滑动变阻器R1(0~20Ω)
E.滑动变阻器R2(0~50Ω)
F.电源E(电动势4.0v,内阻不计)
G.开关s和导线若干
(1)测量过程中他们发现,当电压达到1.23v时,灯泡亮度很弱,继续缓慢地增加电压,当达到2.70v时,发现灯泡已过亮,立即断开开关,所有测量数据见表:
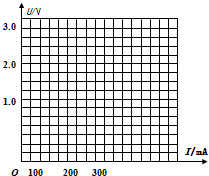
请你根据表中数据,在给出的坐标纸上作出U-I图线,从中可得小灯泡的额定电压应为2.5v(结果保留两位有效数字).这一结果大于实验前的计算结果,原因是灯泡冷态电阻小于正常工作时的电阻.
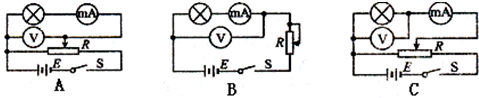
(2)从表中的实验数据可以知道,他们在实验时所选择的电路应为C,电流表应选A2(填“A1”或“A2”),滑动变阻器应选R1(填“R1”或“R2”).
 某实验小组预测定一只小灯泡(其额定功率为0.75w,但额定电压已经模糊不清)的额定电压值,实验过程如下:
某实验小组预测定一只小灯泡(其额定功率为0.75w,但额定电压已经模糊不清)的额定电压值,实验过程如下:他们先用多用电表的欧姆档测出小灯泡的电阻约为2Ω,然后根据公式算出小灯泡的额定电压U=$\sqrt{pR}$≈1.23v.但他们认为这样求得的额定电压值不准确,于是他们利用实验室中的器材设计了一个实验电路,进行进一步的测量.他们选择的实验器材有:
A.电压表V(量程3v,内阻约3kΩ)
B.电流表A1(量程150mA,内阻约2Ω)
C.电流表A2(量程500mA,内阻约0.6Ω)
D.滑动变阻器R1(0~20Ω)
E.滑动变阻器R2(0~50Ω)
F.电源E(电动势4.0v,内阻不计)
G.开关s和导线若干
(1)测量过程中他们发现,当电压达到1.23v时,灯泡亮度很弱,继续缓慢地增加电压,当达到2.70v时,发现灯泡已过亮,立即断开开关,所有测量数据见表:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.20 | 0.60 | 1.00 | 1.40 | 1.80 | 2.20 | 2.70 |
| I/mA | 80 | 155 | 195 | 227 | 255 | 279 | 310 |
(2)从表中的实验数据可以知道,他们在实验时所选择的电路应为C,电流表应选A2(填“A1”或“A2”),滑动变阻器应选R1(填“R1”或“R2”).

14.下列说法正确的是( )
| A. | 物体没做功,则物体就没有能量 | |
| B. | 动摩擦力只能做负功 | |
| C. | 重力对物体做功,物体的重力势能可能增加 | |
| D. | 重力对物体做功,物体的重力势能一定减少 |

 在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.
在“研究匀变速直线运动”的实验中,得到的一条纸带如图所示,纸带上每相邻的两计数点间的时间间隔均为0.1s,测得A到B和B到C的距离分别为5.60cm和8.62cm,则物体的加速度大小为3.02m/s2,B点对应的速度大小为0.711 m/s.